關於矩問題
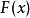 矩問題
矩問題 矩問題
矩問題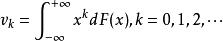 矩問題
矩問題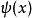 矩問題
矩問題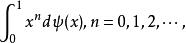 矩問題
矩問題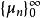 矩問題
矩問題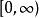 矩問題
矩問題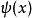 矩問題
矩問題在機率論中,已知分布函式為,對於連續隨機變數的k階原點矩。假設已知它的若干階原點矩,能否求出其分布函式呢?在物理學中,若有一根長為l的細棒,其線密度為,繞一端點旋轉,則分別表示該細棒的質量、靜力矩、轉動慣量等一系列量。我們考慮其逆問題,即若已知細棒的質量、靜力矩、轉動慣量等一系列量,能否確定其密度函式?實際上這就是矩問題給一個矩量序列,在區間找到一個正的有界非減函式使之滿足:
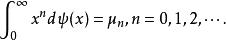 矩問題
矩問題這個問題Stieltjes於1894-1895年提出並得到了解決。
矩問題是一個從世紀開始研究的古典問題,但是基於研究的重要性現在被越來越多的人所重新認識。目前,矩問題的研究把運算元理論、機率論、矩陣論結合起來,同時又與其他的研究方向相聯繫。
矩問題的產生
在數學中,在試圖將一個度量μ映射到序列Mn求結果時就產生了矩問題。Mn表示為:
 矩問題
矩問題更一般地,對任意函式序列Mn可以表示為:
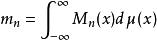 矩問題
矩問題介紹
在經典設定中,μ是實線上的度量,M是序列{xn:n = 0,1,2,...}。 在這種形式中,問題出現在機率論中,詢問是否存在具有指定均值,方差等的機率測度,以及它是否是唯一的。
有三個經典時刻問題:可以將μ的支持作為整個實線的漢堡時刻問題; 對於[0,+∞],Stieltjes矩問題; 並且一個有界區間的Hausdorff時刻問題,而不失一般性可能被認為是[0,1]。
存在性
數字序列mn是若且唯若滿足某個正定條件時測量μ的矩的序列;即Hankel矩陣Hn,
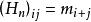 矩問題
矩問題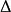 矩問題
矩問題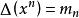 矩問題
矩問題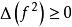 矩問題
矩問題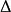 矩問題
矩問題應該是正半定的。這是因為正半定律漢克爾矩陣對應於線性函式,使得,並且。假設可以擴展到R[x*]。在單變數情況下,非負多項式總是寫為平方和。因此,在單變數情況下,線性函式對於所有非負多項式都是正的。通過Haviland定理,線性函式具有度量形式,即:
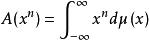 矩問題
矩問題對於給定間隔[a,b]支持的度量mu的存在,類似形式的條件是必需的和足夠的。
證明這些結果的一種方法是考慮將多項式的線性函式:
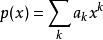 矩問題
矩問題代入到:
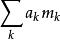 矩問題
矩問題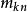 矩問題
矩問題如果是[a,b]上μ支持的矩陣,那么顯然:
對於[a,b]上非負數的任何多項式P,φ(P)≥0。
唯一性
Hausdorff矩問題中的μ的唯一性來自於Weierstrass逼近定理,其中說明在[0,1]的連續函式的空間中,多項式在均勻範數內是密集的。 對於無限間隔的問題,唯一性是一個更微妙的問題。
矩問題的求解
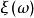 矩問題
矩問題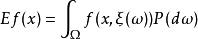 矩問題
矩問題用逼近方法來求解隨機最最佳化問題,核心之一就是廣義矩問題的求解。如逼近法使用的逼近機率測度是一些矩約束下的極值機率測度,根據隨機變數的部分矩信息計算期望函式的上下界的問題等,歸結起來都是解廣義矩問題。故通過分析廣義矩問題及其對偶問題的關係,提出了通過對偶問題來解廣義矩問題的一種新方法。
