歷史
勾股定理（也稱商高定理）是中國古代天文觀測實踐中立竿測影的重大發現，在中國古代數學、天文曆法和工程運用極其廣泛，影響深遠。最早數學著作記述見於《周髀算經》中周公與商高的對話。對話中提及大禹治水時期，勾股定理就已經套用於治水工程中，還延伸至國家建章立制的政治高度—“故禹之所以治天下者，此數之所生也。”
《周髀算經》中記載，周公後人陳子敘述的勾股定理公式為“若求邪至日者，以日下為勾，日高為股，勾股各自乘，並而開方除之，得邪至日”.
《史記•夏本紀》記載大禹治水：“陸行乘車，水行乘船，泥行乘橇，山行乘檋。左準繩，右規矩，載四時，以開九州，通九道，陂九澤，度九山。”其中的規和矩就是運用勾股定理的實用工具之一。
劉徽在《九章算術注》序言中，言及周代運用勾股定理立桿測影：“以南戴日下及日去地為勾、股，為之求弦，即日去人也。以徑寸之筒南望日，日滿筒空，則定筒之長短以為股率，以筒徑為勾率，日去人之數為大股，大股之勾即日徑也。雖夫圓穹之象猶曰可度，又況泰山之高與江海之廣哉。”。這段論述，是勾股定理在古代中國用於立桿測影的佐證之一。
因此，歷代中國數學家對勾股理論非常重視，傾注大量心血進行研究，成果斐然，以東漢末期趙爽勾股弦圖（即：勾股圓方圖）為代表。
2002年第24屆國際數學家大會（ICM）在北京召開。中國郵政發行一枚郵資明信片，郵資圖就是這次大會的會標—中國古代證明勾股定理的趙爽弦圖。
趙爽 勾股圓方圖 方法
劉徽描述此圖，“勾自乘為朱方，股自乘為青方，令出入相補，各從其類，因就其餘不動也，合成弦方之冪。開方除之，即弦也。”其大意為，一個任意直角三角形，以勾寬作紅色正方形即朱方，以股長作青色正方形即青方。將朱方、青方兩個正方形對齊底邊排列，再進行割補—以盈補虛，分割線內不動，線外則“各從其類”，以合成弦的正方形即弦方，弦方開方即為弦長。
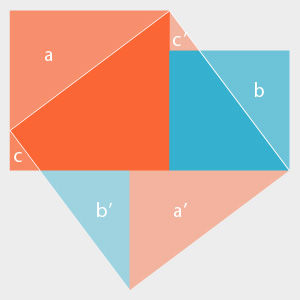劉徽 青朱出入圖 此外，作為中國歷史上最偉大的數學家之一，劉徽作《九章算術注》時，在勾股理論方面逐一論證了有關勾股定理與解勾股形的計算原理，發展了勾股測量術。通過對“勾中容橫”與“股中容直”之類的典型圖形的論析，建立了相似勾股形理論。
評價
青朱出入圖在勾股定理幾何證明中別開生面，不著一字即可讓人心領神會，故與趙爽勾股圓方圖相映成趣，前者縱橫交錯寓圓於方，後者割矩為方巧施損益，為中華先祖最早發現勾股定理在理論上作出了完美之詮釋，是東方智慧的特定產物。
青朱出入圖因其特色鮮明，備受後世矚目。1978年，華羅庚先生修改舊作《大哉數學之為用》，重新以《數學的用場與發展》發表，文中對青朱出入圖給予極高評價：“順順便提一下，如果我們宇宙航船到了一個星球上，那兒也有如我們人類一樣高級的生物存在，我們用什麼東西作為我們之間的媒介？帶幅畫去吧，那邊風景殊，不了解；帶一段錄音去吧，也不能溝通。我看最好帶兩個圖形去：一個‘數’一個‘數形關係’（勾股定理）。為了使那裡較高級的生物知道我們會幾何證明，還可送去上面的圖形，即‘青朱出入圖’。這些都是我國古代數學史上的成就。”
參考文獻
--------------------------------
劉徽《九章算術注》
《周髀算經》
郭書春譯註《九章算術》
