定義
為考察標量場在空間的分布和變化規律,引入等值面、方嚮導數和梯度的概念。標量函式的梯度是一矢量,它的量值就是方嚮導數中的最大值,它的方向即為取得最大方嚮導數時的方向,也即最大增加率的方向,以電位為例,即為電位梯度。
基本原理
在勻強電場裡,我們有V=El(有的版本是U=Ed,就是兩點間的電位差等於電場強度和兩點在場強方向的距離的乘積),把這個等式變換為:E=V/l,我們就可以得出這樣一個結論:電場強度等於電位梯度,並指向電位降落的方向。
理論可以證明,這最後一個結論,不僅對勻強電場適用,而且對任何別種電場也都適用。但由於電位梯度,除勻強電場之外,一般都不等於V/l,所以上面的等式只對勻強電場適用。
在厘米·克·秒制靜電單位系中,電位梯度的單位為靜伏/厘米。勻強電場的電位梯度在數值上等於沿場強方向相隔1厘米兩點間的電位差的靜伏數。
電位梯度在數值上的負值等於該點場強沿相同方向分量。
與電場關係
電位梯度與電場強度間的關係
 電位梯度
電位梯度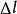 電位梯度
電位梯度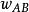 電位梯度
電位梯度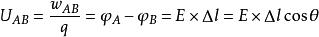 電位梯度
電位梯度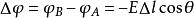 電位梯度
電位梯度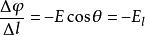 電位梯度
電位梯度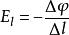 電位梯度
電位梯度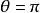 電位梯度
電位梯度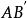 電位梯度
電位梯度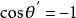 電位梯度
電位梯度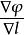 電位梯度
電位梯度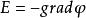 電位梯度
電位梯度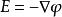 電位梯度
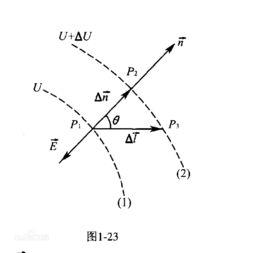
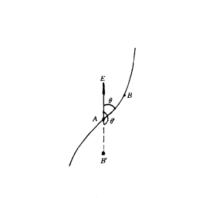
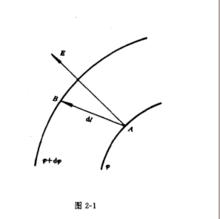
電位梯度如右圖所示,設電場中任意二點A、B間的距離很小,可視為均勻場,單位正電荷由A移到B時電場力做功,A、B間電壓 (1)。今令電位增加量 (2),則 (3)或 (4)。若 (5),即不走AB路徑,而走路徑,則 (6)。最大,即表A點的電位梯度。由圖可知: (7)或 (8)。
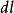 電位梯度
電位梯度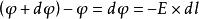 電位梯度
電位梯度 電位梯度
電位梯度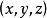 電位梯度
電位梯度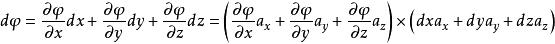 電位梯度
電位梯度如右圖所示,表示A到B的矢量,由電位定義 (9)但為空間坐標的函式,它的全微分是
 電位梯度
電位梯度 電位梯度
電位梯度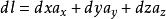 電位梯度
電位梯度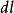 電位梯度
電位梯度 電位梯度
電位梯度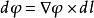 電位梯度
電位梯度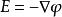 電位梯度
電位梯度(10)也就是說,的全微分可看成兩個矢量點乘的結果,其中 (11)即為從A到B的矢量的直角坐標表達式,根據梯度的定義 (12)於是式(10)即可寫成(13)比較式(9)和(13)有 (14)
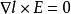 電位梯度
電位梯度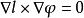 電位梯度
電位梯度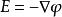 電位梯度
電位梯度事實上我們從靜電場的基本方程及矢量恆等式可以說明 式(14)是正確的。因為靜電場中,又,故是正確的。故靜電場中某點電位梯度與電場強度大小相等,方向相反,它表示某點單位距離中電位升高的最快值。