零級消除動力學

零級消除動力學是藥物在體內以恆定的速率消除，即不論血漿藥物濃度高低，單位時間內消除的藥物量不變。因在半對數坐標圖上的藥-時曲線下降部分呈曲線，故稱非線性動力學（nonlinerkinetics）。通常是因為藥物在體內的消除能力達到飽和所致。

基本信息

• 中文名：零級消除動力學
• 英文名：zero-order elimination kineics

• 歸屬：非線性動力學
• 公式：dC/dt=-k0

介紹

零級消除動力學

從生理學看,體液被分為血漿、細胞間液及細胞內液幾個部分.為了說明藥動學基本概念及規律現假定機體為一個整體,體液存在於單一空間,藥物分布瞬時達到平衡（一室模型）.問題雖然被簡單化,但所得理論公式不失為臨床套用提供了基本規律.按此假設條件,藥物在體內隨時間變化可用下列基本通式表達：dC/dt=kCn.C為血藥濃度,常用血漿藥物濃度.k為常數,t為時間.由於C為單位血漿容積中的藥量（A）,故C也可用A代替：dA/dt=kCn,式中n=0時為零級動力學,n=1時為一級動力學,藥物吸收時C（或A）為正值,消除時C（或A）為負值.在臨床套用中藥物消除動力學公式比較常用,故以此為例如以推導和說明。

區別

零級消除動力學

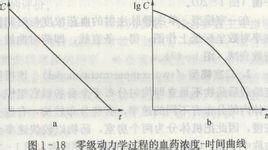
當n=0時,-dC/dt=KC0=K（為了和一級動力學中消除速率常數區別,用K代k）,將上式積分得：
Ct=C0-Kt,C0為初始血藥濃度,Ct為t時的血藥濃度,以C為縱座標、t為橫座標作圖呈直線,斜率為K,當Ct/C0=1/2時,即體內血漿濃度下降一半（或體內藥量減少一半）時,t為藥物消除半衰期（t1/2）.
按公式1/2C0=C0-Kt1/2可見按零級動力學消除的藥物血漿半衰期隨C0下降而縮短,不是固定數值.零級動力學公式與酶學中的Michaelis-Menten公式相似,S為酶的底物,Vmax為最大催化速度,Km為米氏常數.當[S]>>Km時,Km可略去不計,ds/dt=Vmax,即酶以其最大速度催化.零級動力學公式與此一致,說明當體內藥物過多時,機體只能以最大能力將體內藥物消除.消除速度與C0高低無關,因此是恆速消除.例如飲酒過量時,一般常人只能以每小時10ml乙醇恆速消除.當血藥濃度下降至最大消除能力以下時,則按一級動力學消除.

一級動力學過程

(first-orderKineticprocess)一級動力學過程又稱一級速率過程,是指藥物在某房室或某部位的轉運速率(dC/dt)與該房室或該部位的藥量或濃度的一次方成正比.描述一級動力學過程的公式dC――=-KCdt(C為藥物濃度,K為一級速率常數)上式積分,得:C=C0e-kt(C0為藥物起始濃度)上式改為常用對數式,則:KlogC=logC0-――t2.303可見,將t時藥物濃度的對數對時間作圖,可得一條直線,其斜率為-K/2.303.