定義
零空間
零空間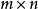 零空間
零空間定義：已知 為一個 矩陣。 的零空間（nullspace），又稱核（kernel），是一組由下列公式定義的 維向量：
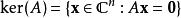零空間
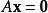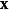零空間
零空間即線性方程組 的所有解 的集合。
在數學中，一個運算元 A的 零空間是方程 A v= 0的所有解 v的集合。它也叫做 A的核，核空間。用集合建造符號表示為
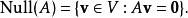零空間例子
零空間（1） 考慮函式 ：
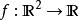零空間
零空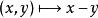間
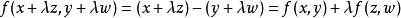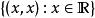零空間
零空間它是一個線性映射，因為 。它的零空間由所有第一個和第二個坐標一致的向量組成，就是說描述了一條直線 。
零空間 零空間（2）在一個線性空間中固定一個向量 並定義線性映射 為向量x 和y 的點積。它的零空間由所有正交於 y 的向量，即 y 的正交補組成。
性質
如果 A是矩陣，它的零空間就是所有向量的空間的線性子空間。這個線性子空間的維度叫做 A的 零化度(nullity)。這可以計算為在矩陣 A的行梯陣形式中不包含支點的縱列數。 秩-零化度定理聲稱任何矩陣的秩加上它的零化度等於這個矩陣的縱列數。
對應於零奇異值的 A的右奇異向量形成了 A的零空間的基。
A的零空間可以用來找到和表達方程 A x= b的所有解( 完全解)。如果 x是這個方程的一個解，叫做 特定解，那么方程的完全解等於它的特定解加上來自零空間的任何向量。特定解依 b而變化，而零空間的向量不是。
要證明這一點，我們考慮每個方向。在一個方向上，如果 A y= b，且 A v= 0，則明顯的 A( y+ v) = A y+ A v= b+ 0= b。所以 y+ v也是 A x= b的解。在其他方向上，如果我們有對 A x= b的另一個解 z，則 A( z− y) = A z− A y= b−b = 0。所以向量 u= z− y在 A的零空間中而 z= y+ u。所以任何解都可以表示為一個零空間中的向量加上特定解 y。
如果一個線性映射 A是單同態，則它的零空間是零。因為如果反過來它的零空間是非零，由類似上面的方法可以得出 A y= b的解不止一個，也就是說線性映射 A不是單射了。
如果映射是零映射，則零空間同於映射的定義域。
矩陣的零空間
考慮矩陣
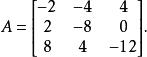零空間要找到它的零空間，須找到所有向量v使得 Av=0。首先把 A 變換成簡約行梯陣形式
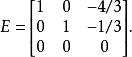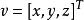零空間
零空間有Av=0若且唯若 Ev=0。使用符號 ，後者方程變為
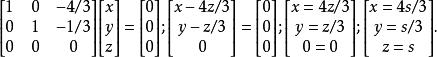零空間所以，A 的零空間是一維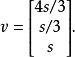空間，
零空間