雙曲守恆律的間斷解
正文
當考察連續介質的運動時，常常導出一階擬線性雙曲型方程組。例如，描述一維理想氣體運動的守恆律組：
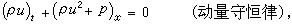
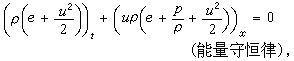
（G.F.）B.黎曼1860年提出了一類最典型的含有間斷的初值問題，即當t=0時在x=0處初值具有一個任意的間斷，而在x>（或<）0時初值分別為常量。這樣的問題稱為黎曼問題。人們很早就研究了上述守恆律方程組的黎曼問題，它的解由向前或向後運動的衝擊波、向前或向後運動的中心疏散波以及接觸間斷所組成。這些波統稱為初等波。
初等波的相互作用也得到了研究。例如，兩個反方向運動的衝擊波相碰後會互相離去，且在它們中間還將出現一個接觸間斷。兩個同方向運動的衝擊波相追總會追上，追上後除合併為一個該方向運動的衝擊波外，還將立即產生一個接觸間斷和一個向反方向運動的衝擊波或中心疏散波。在高維的情形還必須注意馬赫反射的影響等。
一般的擬線性雙曲組為ut+ƒ(u)x＝0，其中u＝(u1,u2,…,un),ƒ＝(ƒ1,ƒ2,…,ƒn)，矩陣
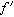(u)有n個相異的實特徵根。 理想氣體可以認為是實際氣體當粘性趨於零時的極限情況。用這種觀點來處理擬線性雙曲組就建立了所謂“粘性消失法”。E.霍普夫最早用此法嚴格論證了單個擬線性方程式初值問題解的大範圍存在性(1950)，以此法為背景，人們還提出了各種差分格式。此外，還有J.馮·諾伊曼等人提出的人工粘性法等等，都是在實際套用中求數值解的常用方法。除氣體力學外，間斷解理論在彈塑性力學、爆震、燃燒等方面都有重要套用。
高維擬線性雙曲型方程組的間斷解問題，在套用上極為重要，但對它們的研究還剛剛在開始。
