定義
 右極限
右極限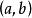 右極限
右極限假設 是定義在區間 上的函式,如果下列準則成立:
 右極限
右極限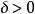 右極限
右極限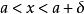 右極限
右極限 右極限
右極限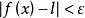 右極限
右極限任意給定 ,能夠找到 ,使得滿足不等式 的一切 ,恆有 。
 右極限
右極限 右極限
右極限 右極限
右極限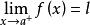 右極限
右極限則稱當 由右邊趨於 時,收斂於極限 。記為 。
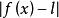 右極限
右極限 右極限
右極限 右極限
右極限 右極限
右極限 右極限
右極限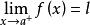 右極限
右極限 右極限
右極限 右極限
右極限 右極限
右極限 右極限
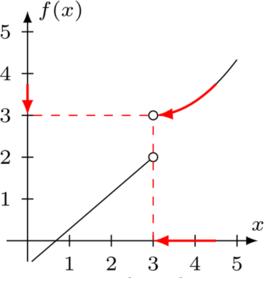
右極限數值 是 與 之間的距離,我們可以認為它是用 近似表示 所產生的誤差。因此 的定義,相當於斷言:用 近似表示 所產生的誤差可以小到我們任意指定的程度,只需要 從坐標充分靠近 。
 右極限
右極限性質
左極限與右極限統稱單側極限。
 右極限
右極限 右極限
右極限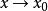 右極限
右極限 右極限
右極限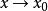 右極限
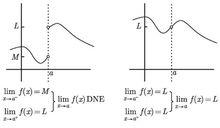
右極限①函式 當 時,極限存在,若且唯若函式在處左極限和右極限都存在,且兩者相等。用數學表達式表示為:
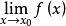 右極限
右極限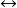 右極限
右極限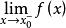 右極限
右極限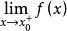 右極限
右極限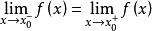 右極限
右極限存在和都存在且。
②函式的左極限和右極限不一定相等,例如:
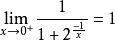 右極限
右極限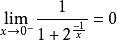 右極限
右極限此時稱函式在該點有“跳躍”。
③左極限與右極限只要有其中有一個極限不存在,則函式在該點極限不存在。