![閏年[曆法中的閏年]](/img/5/f2b/nBnauM3XxcjN5AjN5UjM0IDN2QTMxETMzczMzQTNwAzMwIzL1IzL2gzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg "閏年[曆法中的閏年]")
簡介
閏年閏年（leap year），在公曆（格里曆）或夏曆中有閏日的年份，以及在中國舊曆農曆中有閏月的年份。地球繞太陽運行周期為365天5小時48分46秒（合365.24219天）即一回歸年（tropical year）。公曆的平年只有365日，比回歸年短約0.2422 日，所餘下的時間約為四年累計一天，於第四年加於2月，使當年的歷年長度為366日，這一年就為閏年。
產生原因
閏年在公曆（格里曆）紀年中，有閏日的年份叫閏年，一般年份365天，閏年為366天。由於地球繞太陽運行周期為365天5小時48分46秒（合365.24219天）即一回歸年，公曆把一年定為365天。所餘下的時間約為四年累計一天，加在二月里，所以平常年份每年365天，二月為28天，閏年為366天，二月為29天。因此，每400年中有97個閏年，閏年在2月末增加一天，閏年366天。
中國舊曆農曆紀年中，有閏月的一年稱為閏年。一般年份為12個月，354或355天，閏年則為13個月，383或384天。農曆作為陰陽曆的一種，每月的天數依照月虧而定，一年的時間以12個月為基準；為了合上地球圍繞太陽運行周期即回歸年，每隔2到4年，增加一個月，增加的這個月為閏月，因此農曆的閏年為13個月。
農曆沒有第十三月的稱謂，閏月按照曆法規則，排放在從二月到十月的過後重複同一個月，重複的這個月為閏月，如四月過後的閏月稱為閏四月。
農曆閏年閏月的推算，3年一閏，5年二閏，19年七閏；農曆基本上19年為一周期對應於公曆同一時間。如公曆的2001年5月27日、1982年5月27日和1963年5月27日這個日子，都是閏四月初五。
閏月加到哪個月，以農曆曆法規則推斷，主要依照與農曆的二十四節氣相符合來確定；農曆的閏月天數與正常月份天數一樣，為29或30天。農曆所謂“閏”的說法，只有閏年和閏月稱謂，公曆也有閏年的稱謂。
雙閏年
通常情況下，每4年會出現一次陽曆閏年，每19年會有7次農曆閏年，兩個閏年一旦重合，就是雙閏年了。
判定方法
判定公曆閏年遵循的一般規律為：四年一閏，百年不閏，四百年再閏。
公曆閏年的精確計算方法：（按一回歸年365天5小時48分45.5秒）
①、普通年能被4整除而不能被100整除的為閏年。 （如2004年就是閏年，1900年不是閏年）
②、世紀年能被400整除而不能被3200整除的為閏年。 (如2000年是閏年，3200年不是閏年)
③、對於數值很大的年份能整除3200,但同時又能整除172800則又是閏年。(如172800年是閏年，86400年不是閏年）
公元前閏年規則如下：
1、非整百年：年數除4餘數為1是閏年，即公元前1、5、9……年；
2、整百年：年數除400餘數為1是閏年，年數除3200餘數為1，不是閏年,年數除172800餘1又為閏年，即公元前401、801……年。
分類介紹
閏年包括在公曆（格里曆）或夏曆中有閏日的年份，和在中國農曆中有閏月的年份。
公曆閏年
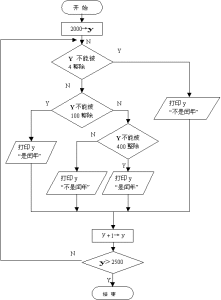閏年計算流程圖現在的公曆是根據羅馬人的“儒略曆”改編而得。由於當時沒有了解到每年要多算出0.0078天的問題，從公元前46年，到16世紀，一共累計多出了10天。為此，當時的教皇格雷果里十三世，將1582年10月5日人為規定為10月15日。並開始了新閏年規定。即規定公曆年份是整百數的，必須是400的倍數才是閏年，不是400的倍數的就是平年。此後，平均每年長度為365.2425天，約4年出現1天的偏差。按照每四年一個閏年計算，平均每年就要多算出0.0078天，經過四百年就會多出大約3天來，因此，每四百年中要減少三個閏年。閏年的計算，歸結起來就是通常說的：四年一閏；百年不閏，四百年再閏。
由於地球的自轉速度逐漸降低，而公轉速度則相對更加穩定，所以上述的系統經過更長的周期也會發生微小的誤差。據計算，每8000年會有一天的誤差，所以英國的天文學家John Herschel提議公元4000為平年，以後類推12000年，20000年亦為平年。但此提議從未被正式採納。原因是到了4000年，地球自轉的精確速度並非現在可以預測，所以屆時參照真實數據方可做出判斷。因此，在長遠的將來，針對閏年的微小調整應該不是由預定的系統決定，而是隨時不定性的。
西方公曆閏年
陽曆中有閏日的年份叫閏年，相反就是平年，平年為365天，閏年為366天。在公曆（格里曆）紀年中，平年的二月為28天，閏年的二月為29天。閏年平月2月29日為閏日。
中國農曆閏年
中國舊曆農曆作為陰陽曆的一種，每月的天數依照月虧而定，一年的時間以12個月為基準，平年比一回歸年少約11天。為了合上地球圍繞太陽運行周期即回歸年，每隔2到4年，增加一個月，增加的這個月為閏月。閏月加到哪個月，以農曆曆法規則推斷，主要依照與農曆的二十四節氣相符合來確定。在加有閏月的那一年有13個月，歷年長度為384或385日，這一年也稱為閏年。如1984年鼠年的農曆中，有兩個十月，通常成為前十月和後十月（即閏月）。農曆閏年閏月的推算，3年一閏，5年二閏，19年七閏；農曆基本上19年為一周期對應於公曆同一時間。如公曆的2001年5月27日、1982年5月27日和1963年5月27日這個日子，都是閏四月初五。
公曆與農曆
公曆1982年至2042年與農曆閏年閏月對照表| 1982年5月23日閏四月小壬戊年 1984年11月23日閏十月大甲子年 1987年7月26日閏六月大丁卯年 1990年6月23日閏五月大庚午年 1993年4月22日閏三月大癸酉年 1995年9月25日閏八月大乙亥年 1998年6月24日閏五月小戊寅年 2001年5月23日閏四月大辛巳年 2004年3月21日閏二月大甲申年 2006年8月24日閏七月大丙戊年 2009年6月23日閏五月大己丑年 2012年5月21日閏四月小壬辰年 2014年10月24日閏九月小甲午年 2017年7月23日閏六月大丁酉年 2020年5月23日閏四月小庚子年 2023年3月22日閏二月大癸卯年 2025年7月25日閏六月大己巳年 2028年6月23日閏五月大戊申年 2031年4月22日閏三月大辛亥年 2033年8月25日閏七月大癸丑年 2036年7月23日閏六月小丙辰年 2039年6月22日閏五月大己未年 2042年3月22日閏二月大壬戊年 |
計算方法
程式計算
Java語言：publicbooleanisLeapYear(intyear){return(year%4==0&&year%100!=0)||year%400==0;}
VB語言：
PublicFunctionisLeapYear(yearAsInteger)AsBoolean
isLeapYear=(yearMod4=0AndyearMod100<>0)OryearMod400=0
EndFunction
C語言：
#include<stdio.h>
intmain()
{inty;printf("請輸入年份，回車結束\n");scanf("%d",&y);if((y%4==0&&y%100!=0)||y%400==0)
{printf("%d是閏年",y);}else
{printf("%d是平年",y);}
return0;}
精確計算方法
（按一回歸年365天5小時48分45.5秒）①、普通年能被4整除且不能被100整除的為閏年。（如2004年就是閏年,1901年不是閏年）
②、世紀年能被400整除的是閏年。(如2000年是閏年，1900年不是閏年)
③、對於數值很大的年份,這年如果能整除3200,並且能整除172800則是閏年。如172800年是閏年，86400年不是閏年(因為雖然能整除3200，但不能整除172800)（此按一回歸年365天5h48'45.5''計算）。
此外，如依照現有太陽年的長度與上述閏年規則，每8000年又約差一日，因此約翰·赫歇爾提議每逢4000的倍數不閏，如西元4000年。但距此一年份來臨尚有約二千年之遙，因此還未曾真正納入規則或實施過。又由於地球公轉速率的不穩定與眾多影響因素，屆時是否需要納入此規則仍有疑問。
原因：若一年按365天5h48'46''（此時86400年也是閏年）計算，一年日數必須是整數，不便將零時數計入，所以取365天為一年，則餘5時48分46秒，積至4年約滿一日，所以4年一“閏日”，謂之“閏年”，無“閏日”之年為平年，即平年365天，閏年366天。但到4年之時，僅有23時15分4秒閏一日，欠缺44分56秒；積至100年（25閏）時就欠缺18時43分20秒，約合3/4日，所以滿100年不閏；此時又餘5時16分40秒，積至400年餘21時6分40秒又閏；又欠缺2時53分20秒，積至3200年計欠缺23時6分40秒，所以滿3200年不閏；此時又餘53分20秒，積至86400年剛好24時又一閏，這是不余不欠，需重計算，所以按陽曆計算就有上面的閏年規則。
按一回歸年365天5h48'45.5''計算：3200年多出16000小時153600分145600秒=18600小時26分40秒，共32*24+8=136個閏年=776*24=18624小時>18600小時，所以只能算到775個閏年，3200不是閏年，於是775*24=18600，多出了26分40秒怎么辦需要多少個周期彌補？答案是54個周期，為172800年，因為172800/3200=54個周期54*26分40秒=1404分2160秒=24小時。
祖沖之改革
在古代，我國曆法家一向把十九年定為計算閏年的單位，稱為“一章”，在每一章里有七個閏年。也就是說，在十九個年頭中，要有七個年頭是十三個月。這種閏法一直採用了一千多年，不過它還不夠周密、精確。公元412年，北涼趙厞創作《元始歷》，才打破了歲章的限制，規定在六百年中間插入二百二十一個閏月。可惜趙厞的改革沒有引起當時人的注意，例如著名歷算家何承天在公元443年製作《元嘉歷》時，還是採用十九年七閏的古法。祖沖之吸取了趙厞的先進理論，加上他自己的觀察，認為十九年七閏的閏數過多，每二百年就要差一天，而趙厞六百年二百二十一閏的閏數卻又嫌稍稀，也不十分精密。因此，他提出了三百九十一年內一百四十四閏的新閏法，這個閏法在當時算是最精密的了。
除了改革閏法以外，祖沖之在曆法研究上的另一重大成就，是破天荒第一次套用了“歲差”。
”祖沖之在曆法研究方面的第三個巨大貢獻，就是能夠求出曆法中通常稱為“交點月”的日數。
祖沖之根據上述的研究成果，終於成功製成了當時最科學、最進步的曆法——《大明曆》。這是祖沖之科學研究的天才結晶，也是他在天文曆法上最卓越的貢獻。
