開爾文最小能量定理

開爾文最小能量定理是流體力學中有關不可壓縮無粘性流體運動的一個定理。該定理揭示了在所作的假設下，無旋運動由於具有最小能量因而成為最優的運動形態，加深了對無旋運動特性的了解。

開爾文最小能量定理

正文

流體力學中有關不可壓縮無粘性流體運動的一個定理。內容是：若在單聯通區域τ的邊界S上，無旋運動和有旋運動具有相同的法向速度，則無旋運動的動能（見能）恆小於有旋運動的動能。此定理可證明如下：令有旋運動和無旋運動的速度矢量和動能分別為v、T┡和墷Ф、T，並設v0＝v－墷Ф。顯然v0不恆等於零,否則有旋運動和無旋運動恆同,這是不可能的。根據定理的假設,在邊界S上有v0·n＝0，其中n為邊界S的法向單位矢量。根據連續性方程有墷·v0＝0。顯然下式成立：

因為墷·v0＝0，所以v0·墷Ф＝墷·(Фv0)，對上式中第二個積分套用高斯定理並考慮到在邊界S上v0·n＝0，得：

。

注意到v0不恆等於零，上式中第一個積分是一個不等於零的正數。由此得到開爾文最小能量定理的結論:T┡>T。
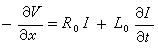開爾文最小能量定理揭示,在定理所作的假設下,無旋運動由於具有最小能量因而成為最優的運動形態，從而加深了對無旋運動特性的了解。

配圖

相關連線