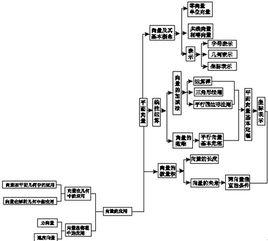
同角三角函式間的基本關係式:
平方關係:
sin^2(α)+cos^2(α)=1
tan^2(α)+1=sec^2(α)
cot^2(α)+1=csc^2(α)
積的關係:
sinα=tanα*cosα
cosα=cotα*sinα
tanα=sinα*secα
cotα=cosα*cscα
secα=tanα*cscα
cscα=secα*cotα
倒數關係:
tanα·cotα=1
sinα·cscα=1
cosα·secα=1
直角三角形ABC中
說明
銳角角A的正弦(sin),餘弦(cos)和正切(tan),餘切(cot)以及正割(sec),(餘割csc)都叫做角A的銳角三角函式。
正弦(sin)等於對邊比斜邊;
餘弦(cos)等於鄰邊比斜邊;
正切(tan)等於對邊比鄰邊;
餘切(cot)等於鄰邊比對邊;
正割(sec)等於斜邊比鄰邊;
餘割 (csc)等於斜邊比對邊。
兩角和與差的三角函式:
cos(α+β)=cosα·cosβ-sinα·sinβ
cos(α-β)=cosα·cosβ+sinα·sinβ
sin(α±β)=sinα·cosβ±cosα·sinβ
tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)
tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)
輔助角公式:
Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中
sint=B/(A^2+B^2)^(1/2)
cost=A/(A^2+B^2)^(1/2)
倍角公式:
sin(2α)=2sinα·cosα=2/(tanα+cotα)
cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)
tan(2α)=2tanα/[1-tan^2(α)]
三倍角公式:
sin(3α)=3sinα-4sin^3(α)
cos(3α)=4cos^3(α)-3cosα
半角公式:
sin(α/2)=±√((1-cosα)/2)
cos(α/2)=±√((1+cosα)/2)
tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα
降冪公式
sin^2(α)=(1-cos(2α))/2=versin(2α)/2
cos^2(α)=(1+cos(2α))/2=vercos(2α)/2
tan^2(α)=(1-cos(2α))/(1+cos(2α))
萬能公式:
sinα=2tan(α/2)/[1+tan^2(α/2)]
cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]
tanα=2tan(α/2)/[1-tan^2(α/2)]
積化和差公式:
sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]
cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]
cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]
sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]
和差化積公式:
sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]
其他:
sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0
cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及
sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2
tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0
思考:
1.銳角三角函式與解直角三角形直接相關。鈍角三角函式則與解任意三角形直接相關,任意角的三角函式雖然是銳角,鈍角三角形的推廣,它是基本的,有表現力的周期函式。
2.正弦函式,餘弦函式的基本性質與圓的幾何性質存在著緊密的聯繫。將角放在直角坐標系中不但使角的表示有了統一的方法,而且使我們能夠藉助直角坐標系中的單位圓,建立角的變化與單位園上點的變化之間的對應關係,從而用單位圓上點的縱坐標,橫坐標表示圓心角的正弦函式,餘弦函式。
3.勾股定理與同角三角函式的基本關係有內在的一致性,圓的各種對稱性與三角函式奇偶性,誘導公式等也是一致的。
4.三角函式的研究過程能過很好的體現數形結合的思想。利用三角函式數形結合也可以很好的解決一些物理問題。