定義
以量子力學為基礎的統計力學，稱為量子統計力學。經典統計力學以經典力學為基礎，因而經典統計力學也具有局限性。例如：隨著溫度趨於絕對零度，固體的熱也趨於零的實驗現象，就無法用經典統計力學來解釋。
在巨觀世界中，看起來相同的物體總是可以區別的，在微觀世界中，同一類粒子卻無法區分。例如：所有的電子的一切性質都完全一樣。在巨觀物理現象中，將兩個巨觀物體交換，就得到一個和原來狀態不同的狀態，進行統計時必須將交換前和交換後的狀態當作兩個不同的狀態處理；但是在一個物理系統中，交換兩個電子後，得到的還是原來的狀態，因此進行統計時，必須將交換前和交換後的狀態當作同一個狀態來處理。
在巨正則系統下的研究
量子統計的主要任務是從相互作用出發求出熱力學函式，在巨正則系統下的研究結果如下：
巨配分函式
利用拉格朗日不定乘子法，在3個約束條件（機率歸一，能量與粒子數平均值的表達式）下，求熵的極值（平衡態下熵取最大值），再與巨勢滿足的方程比較，得到巨配分函式：
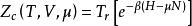量子統計力學
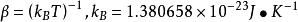量子統計力學
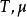量子統計力學
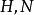量子統計力學
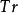量子統計力學式中 為玻爾茲曼常數，它是熱力學與統計物理學的標誌性常數； 分別為溫度與化學勢； 分別為哈密頓算符與粒子算術符； 是陣跡符號。
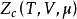量子統計力學
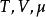量子統計力學顯然 是變數 的函式，而不是一個算符，它可以在任一祖方便的基底下寫出來。
基本方程
量子統計力學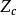
量子統計力學量子統計理論給出了巨勢 與巨配分函式 之間的關係，即量子統計的基本方程為：
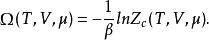量子統計力學密度矩陣
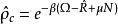量子統計力學密度矩陣的定義為： 。
分類
量子統計力學分為非平衡統計力學與平衡統計力學兩大類。平衡統計力學研究平衡系統的統計規律，已有比較成熟的理論。 非平衡態量子統計力學研究一個量子多體系統從非平衡態趨向平衡態的時間演化過程。因為這一演化是由量子動力學規律驅動的，所以它可以用馮·諾意方程來描述。又因為量子統計力學的任務是從微觀量計算巨觀統計熱力學量，所以必須對系統的力學量及其平均值，如能量、動量等，同時對時間、空間坐標選擇一個微觀大，巨觀小的區間。這個區間在微觀上必須足夠大，以至於包含成千上萬個粒子的貢獻，因而可以做統計平均；而這個區間在巨觀上又必須足夠小，因而可以進行巨觀意義上的微分運算，從而建立起用微分方程表示的巨觀統計熱力學定律。
