簡介
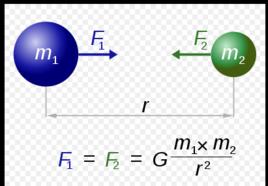
人類對引力的認識始於對行星運動的觀測。德國天文學家克卜勒(Johannes Kepler)根據丹麥天文學家第谷(Tycho Brahe)的大量翔實的觀測資料總結出行星運動三大定律,完美地描述了行星繞太陽運行的運動規律,卻沒有指出行星沿橢圓軌道運動的原因。大約半個世紀以後,牛頓(IsaacNewton)在此基礎上提出了萬有引力定律。此定律不僅對克卜勒三定律提供了動力學的解釋,而且指出維繫行星沿橢圓軌道運動的力和地球上使蘋果落地的力在本質上是相同的。這種力無處不在,小到基本粒子大到宇宙天體,被稱之為“萬有引力”。
1687年,牛頓在《自然哲學的數學原理》(Mathe-matical Principles of Natural Philosophy)一書中系統地介紹了萬有引力定律,其內容如下:宇宙間任何兩個質點都存在相互吸引力,其大小與兩質點的質量m1,m2乘積成正比,與它們之間距離r的平方成反比,用數學表示為
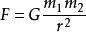 重力常數
重力常數式中的比例係數G稱為萬有引力常數(Universal Gravitational Constant)。它是一個普適常數,不受物體的大小、形狀、組成等因素的影響。引力常數G是一個與理論物理、天體物理和地球物理等密切相關的物理學基本常數。它與天體運動、天體演化和結構模型等有著密切的關係[2]。在粒子與場論、宇宙學以及引力物理的現代理論研究中,G都起著非常重要的作用。譬如描述自然界基本常數體系的Planck長度、時間以及質量就是由三個基本物理量Planck常數ħ、萬有引力常數G、以及光速c的不同組合給出。
自從牛頓的《自然哲學的數學原理》發表300多年以來,萬有引力的理論與實驗研究一直是科學界的熱點之一。理論工作者致力於研究引力的本質、起源及其在物理學中所起的作用,試圖統一四種基本相互作用。實驗工作者則對該定律提出一系列的問題,例如:G的精確值是多大?它是一個常數還是會隨時間和地點而變化?引力是嚴格地與距離的平方成反比嗎?它與兩物體的組成相關嗎?引力與物體的運動狀態有關嗎?等等。儘管把G引入日益增多的物理學和天體物理學討論中得到的結果會各不相同,但對G進行深入的研究都有助於對引力相互作用性質的認識。曾任劍橋大學Cavendish實驗室主任的Cook教授甚至提出G能否如同國際單位中的光速一樣被當作測量系統中的基本常數的問題。他還提出若有可能將其定義為基本常數,那么對G的測量精度必須有更高的要求 。
歷史
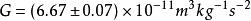 重力常數
重力常數關於引力研究的早期實驗都是採用地球物理方法,其目的停留在為了測量地球的平均密度上,但是這種方法所固有的與地質特性相關的誤差使其不可能給出較高的精度。1798年,Cavendish在當時的英國皇家協會會刊(哲學)(Philos Trans R Soc London)上發表了題為“地球密度的實驗確定”(Experiments to Determine the Density of the Earth)的著名文章。他在文章中介紹了如何使用Michell製作的扭秤(Torsion Balance)研究實驗室內兩物體之間的萬有引力,並首次精確地給出地球的密度是水的密度的5。48倍這一結論,後人由此給出該實驗對應的G值為 。因此,我們常說Cavendish是歷史上第一個“稱量”了地球質量的人,他也因此成為歷史上第一個測量萬有引力常數G的科學家。
繼Cavendish之後,具有代表性的測G工作當屬1895年Boys的實驗,其原理與Cavendish扭秤方法完全相同。直到1942年,他們的結果才被Heyl採用扭秤周期法測量的結果所取代[25,26]。Heyl提出的採用扭秤周期法測量萬有引力常數G的最大優點是將對弱力的測量轉化為對時間的測量。由於對時間的精確測量比較容易實現,因此Heyl給出的G值具有較高的精度,可以說他的測量結果的問世標誌著G絕對值的精確測量的開始。國際上至今仍有幾個小組在採用該方法進行G的測量。
20世紀後半葉,與科學史上其他時期相比,人類進行了更多的測量引力常數的研究工作。科學家們不僅關注引力常數的絕對值,而且也關注引力常數隨時空的變化以及與引力有關的一些反常現象。20世紀80年代以前的這些實驗研究工作已有很多學者做了有益的總結[27~31]。
測量困難
在過去的200多年中,人們在萬有引力常數G的測量過程中付出了極大的努力,但引力常數G測量精度的提高卻非常緩慢,幾乎是每一個世紀才提高一個數量級。這一領域的研究進展之所以如此緩慢,其原因是眾所周知的。首先,萬有引力是自然界四種基本相互作用力中最微弱的。例如,一個電子與一個質子之間的電磁相互作用約是它們之間的萬有引力相互作用的1039倍。微弱的引力信號極易被其他干擾信號所湮沒,因此在實驗中必須克服電磁力、地面振動、溫度變化等因素對實驗的干擾,測量必須在一些採取特別措施的實驗室進行。其次,萬有引力是不可禁止的,因此檢驗質量必然會受到除了實驗專門設定的吸引質量以外的其他物體的引力干擾,比如實驗儀器、實驗背景質量、實驗人員等。另外,移動的質量體,如實驗室附近駛過的車輛以及行人都會給實驗帶來引力擾動。即使在十分偏僻安靜的實驗室,雲層氣壓、雨雪等天氣的變化等都會干擾測量結果。第三,到目前為止,還沒發現G與任何其他基本常數之間存在確定的聯繫,因此不可能用其他基本常數來間接確定G值,只能根據牛頓萬有引力定律。第四,實驗精度受到了測量儀器精度的限制。目前G的測量精度基本上代表了現有機械加工與測量的水平。最後,用於探測微弱引力的工具,如各種形式的扭秤和天平等,存在各種寄生耦合效應和系統誤差,最終限制了測量精度的提高。
測量方法
概述
萬有引力常數G的測量大致可分為地球物理學方法測量、空間測量、實驗室內測量等三大類。地球物理學方法測量G是利用大的自然物體(如形狀規則的山體、礦井和湖泊等)作為吸引質量[12,13]。該方法的主要優點是作為吸引質量的自然物體很大,引力效應明顯。但由於吸引質量的尺度、密度及其分布等都不能精確測量,所以實驗的精度比較低。隨著航天技術的發展,人們期望在太空開展測G實驗[49~53]。空間測量方法可以避免地面實驗室中遇到的兩大難題:一個是地面實驗環境中的附加背景引力場作用,另一個是地面振動噪聲的干擾,但就目前的情況來看,空間測量G的方法面臨著很多新的技術難題,仍在探索之中。實驗室內測量萬有引力常數G的常用工具是精密扭秤和天平。與地球物理學方法相比,精密扭秤的最大優點是將待測的檢驗質量與吸引質量之間的萬有引力相互作用置於與地球重力場方向正交的水平面內,這樣就在實驗設計上極大地減少了重力及其波動的影響[54]。天平可以繞刀口在垂直面內上下傾斜以探測垂直方向的引力作用[55~57]。常用的測量方法有:直接傾斜法、補償法、共振法、周期法和自由落體法等 。
扭秤周期法
一個自由懸掛的扭秤,其運動方程可以寫成諧振子的形式:
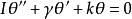 重力常數
重力常數(2)
其中I為扭秤的轉動慣量,γ為阻尼係數,k為扭絲的扭轉彈性係數。扭秤的本徵頻率為
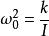 重力常數
重力常數(3)
 重力常數
重力常數如果在扭秤附近放置大的吸引質量,如圖(a)所示,當吸引質量Ma,Mb的連線與扭秤平衡位置平行時(近程配置),吸引質量對檢驗質量的吸引力為扭秤系統提供附加的正回復力矩,使得總回復力矩增大,其振動頻率變為
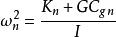 重力常數
重力常數(4)
其中下標n表示近程配置,Kn為懸絲在此配置下的彈性係數,Cgn為由吸引質量與檢驗質量的質量分布決定的引力耦合常數,I為扭秤的轉動慣量。如圖2(b)所示,當吸引質量Ma,Mb的連線與扭秤平衡位置垂直時(遠程配置),吸引質量對檢驗質量的吸引力為扭秤系統提供附加的負回復力矩,使得總回復力矩減小,其振動頻率變為
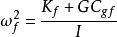 重力常數
重力常數(5)
下標f表示遠程配置。通過測量兩種配置下扭秤的周期而確定G值:
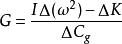 重力常數
重力常數(6)
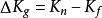 重力常數
重力常數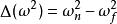 重力常數
重力常數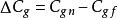 重力常數
重力常數其中 , 為扭絲的滯彈性效應[58]。
扭秤周期法測G是1931年由Heyl提出[25],並和他的同事發展起來的。1942年Heyl等人[26]採用扭秤周期法測量的G值被國際科技數據委員會作為CODATA-73中G值的首次推薦值。在隨後CODATA-86調整時,Cohen和Taylor[33]採用扭秤周期法的測量精度進一步提高,因此作為新一輪G值的推薦值。近三次CODATA收錄的LANL-97,TR&D-98(TR&D-96)和HUST-99(HUST-05)都是採用扭秤周期法。
扭秤周期法是一種動態測量方法,利用了扭秤靈敏度高的優點,而且將一些較難測量的物理量(如幾何量角位移θ)轉化為其他相對較為容易測量的物理量(如時間),可以獲得較高的測量精度。扭秤周期法中的幾何參量,如轉動慣量I、引力耦合常數Cg的測量並不涉及扭秤的運動,測量起來相對容易和方便。與其他利用扭秤的實驗方法相比(如直接傾斜法),周期法對扭秤平衡位置的漂移不是十分敏感。扭秤周期法實際上利用了“差分”的原理,所有在近遠程配置中相同(或者變化規律相同)的參量對實驗結果的影響均被抵消。
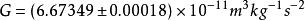 重力常數
重力常數當然,扭秤周期法也存在一些困難。高靈敏度扭秤的周期一般較長,因而所需測量時間也較長,從而對外界環境的穩定性提出了更高的要求。扭秤要達到一個較穩定的狀態需要很長的時間,必須測量較長時間間隔內扭秤的運動狀況方能給出精確的頻率差。而在長時間的測量過程中,背景環境的變化(如溫度)可能就會比較大,這不可避免地對實驗產生影響。此外,扭秤周期法對扭絲是極其依賴的。對所選用懸絲(金屬絲或石英絲)的各種特性深入的研究在扭秤周期法實驗中占據著重要的地位。在我們採用扭秤周期法測G的最新實驗中[46,47],對扭絲的熱彈性[59,60]、非線性[61,62]、滯彈性[58]、老化等效應以及扭秤周期高精度提取方法[63~66]進行了深入的分析與研究。尤其是在實驗中我們利用一根Q值為3.6×10^5的石英絲首次直接對滯彈性效應進行了測量[58],測量結果與1995年Kuroda給出的滯彈性假設(滯彈性效應對G值的修正量為1/πQ)在誤差範圍內吻合[67]。我們實驗小組採用扭秤周期法測量的實驗結果HUST-99(HUST-05)被近三次CODATA收錄。我們最新的測G實驗[46,47]給出的G值為,相對不確定度達到26ppm。該結果是目前國際上採用扭秤周期法測G給出的精度最高的實驗結果,也是目前國際上相對精度優於50ppm的六個實驗結果之一。
扭秤角加速度補償法
扭秤角加速度補償法測量萬有引力常數G的基本原理如圖3所示。讓作為檢驗質量的扭秤處在一個球狀吸引質量的多極引力場中,其角加速度可表示為
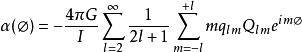 重力常數
重力常數(7)
其中lmq為扭秤的多極矩,lmQ為吸引質量球的多極矩,I為扭秤的轉動慣量,Φ為吸引質量與扭秤之間相對位置的相位差。在公式(7)中,由於高階項衰減很快,角加速度效應最大的項為
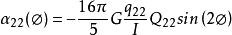 重力常數
重力常數(8)
扭秤的多極矩與轉動慣量之間滿足如下關係:
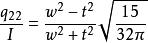 重力常數
重力常數(9)
其中w,t為扭秤的寬度和厚度。當扭秤是一個理想的上下對稱的薄二維平板時,(9)式可近似表示為
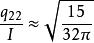 重力常數
重力常數(10)
因此:
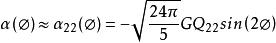 重力常數
重力常數(11)
若將扭秤與吸引質量分別置於兩個獨立的轉台上鏇轉起來,讓扭秤獲得一個慣性力矩Iβ(β為扭秤轉台轉動的加速度)和引力力矩τ=GCg,此時扭秤的運動方程變為
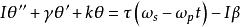 重力常數
重力常數(12)
其中ωs,ωp分別為吸引質量迴轉台和扭秤迴轉台的角速度。通過調整兩個轉台的轉動速度,使扭秤受到的慣性力矩補償吸引質量對扭秤產生的引力力矩,讓扭秤始終處於其平衡位置不動,此時有Iβ=GCg。通過記錄扭秤轉動的加速度,並計算扭秤的轉動慣量I、以及與吸引質量之間的引力耦合係數Cg,就可以給出G值。
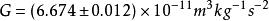 重力常數
重力常數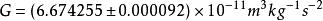 重力常數
重力常數1969年,Rose等人[68]提出扭秤角加速度補償法測G實驗方法,並採用該方法進行了初步實驗。考慮各種誤差因素以後,他們得到的結果為。他們同時指出一系列的改進措施,並聲稱該方法有可能將實驗精度進一步提高兩個數量級。由於該方法中系統的複雜性,在此後的相當長時間內國際上沒有人繼續採用該方法進行測G實驗。直到20世紀末,美國華盛頓大學的Gundlach等人[69,70]改進了扭秤角加速度補償法,提出將吸引質量放置到另一個轉台上也轉動起來,並實現兩個轉台的高精度跟蹤,這樣做的優點是能夠有效減小實驗環境背景引力場的影響。通過對實驗系統的進一步最佳化設計,2000年Gundlach和Merkowitz給出的實驗結果為[42](Uwash-00),相對不確定度優於14ppm,該結果是目前國際上報導的最高精度的測G結果。扭秤角加速度補償法中通過採用一系列的最佳化配置(主要是對稱性),可以極大降低對扭秤幾何尺寸和密度均勻性的測量要求。與扭秤周期法相比,該方法中的懸絲相對於檢驗質量不扭轉,因此實驗結果對懸絲的依賴程度有所降低,尤其是周期法中不可避免的滯彈性效應得到很大程度的抑制[58]。實驗的測量量是角加速度α22,由其他原因引起的恆定角位移或角速度對結果就不會有影響,特別是懸絲的蠕變,其影響可以忽略。由於引力力矩非常小,由此引起的角加速度也非常小,這意味著角速度的變化非常緩慢,因此測量精度可以很高。實驗不需要長時間的測量便可獲得一個好的測量結果,測量時間要比周期法短很多。實驗中由於吸引質量也是在鏇轉的,這樣背景引力場就自然地被平均掉,對實驗結果的影響很小。
扭秤角加速度補償法的缺點是實驗系統非常複雜,需要配置高精度的轉台,通過對系統的閉環控制實現扭秤相對轉台保持相對靜止。實驗中,迴轉台的轉速穩定性需要達到10^-7rad/s量級,兩迴轉台的角加速度差穩定性需要達到10^-12rad/s2量級,這對迴轉台自身提出了很高的要求。同時,外界環境的干擾,如溫度、壓力、磁場和振動等等,仍然都會對實驗結果有影響。
扭秤直接傾斜/補償法
 重力常數
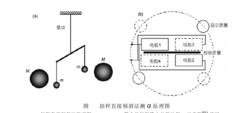
重力常數扭秤傾斜法測G實驗的一般裝置如圖(a)所示。在扭秤的扭臂兩端懸掛著質量均為m的檢驗質量,扭臂用懸絲懸掛。在距離檢驗質量r的水平位置上,放置兩個較大的吸引質量M。由於吸引質量的引力作用,扭秤的平衡位置將產生一個θ的偏轉角,此時扭絲的回覆力矩與引力矩平衡,通過對θ角以及扭秤系統有關參量的測量便可計算出引力常數G:
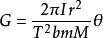 重力常數
重力常數(13)
其中I是扭秤的轉動慣量,T是扭秤的擺動周期,b是扭秤的半臂長。在直接傾斜法實驗中,要求對角進行絕對測量,由θ角的誤差引起的G的測量誤差為
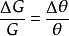 重力常數
重力常數(14)
吸引質量和檢驗質量中心的距離r引起的G值的測量誤差為
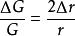 重力常數
重力常數(15)
r的值是通過角的測量得到的,因此θ角的誤差就傳遞到了r上,而且還放大了2倍。θ角本身就很小(mrad量級),而且不可能測得很準,θ就會偏大,所以帶來的誤差很大。如果想增大θ角,唯有增大吸引質量,但是使用大的吸引質量又會影響整個裝置的穩定性,如使裝置傾斜,帶來其他的誤差。此外,引力力矩的測量是通過測量與之平衡的扭絲的扭轉力矩來實現的,因此扭轉力矩的穩定性相當重要。扭轉力矩對溫度變化很敏感,而且扭絲材料本身的缺陷也會使扭絲運動不規則,還有扭絲本身的非線性、熱彈性和老化等效應也會產生誤差。除扭絲自身因素影響之外,周圍環境物體的變化都會造成其平衡位置的漂移。
靜電補償法的原理與直接傾斜法類似,所不同的是使用了額外的靜電力矩補償了引力力矩,使扭絲保持原來的靜止狀態。將直接傾斜法中角位移的直接測量轉換為電信號的測量,測量就相對容易一些。由於扭絲只起到懸掛檢驗質量的作用,並沒有參與測量,所以扭絲的非線性等因素不會影響到實驗結果。由於靜電補償法仍然是靜態的方法,即使引力力矩被靜電力矩平衡了,受外界的干擾扭秤也不可能完全靜止。此外,理想平行板電容的計算很簡單,而實際電容的計算則相當複雜,特別是邊界效應的影響。
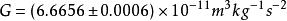 重力常數
重力常數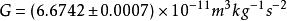 重力常數
重力常數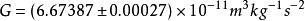 重力常數
重力常數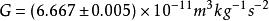 重力常數
重力常數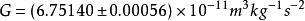 重力常數
重力常數繼Cavendish之後,很多實驗物理學家均採用扭秤傾斜法進行G的測量。紐西蘭國家標準實驗室的Fitzgerald和Armstrong[71]自1995年開始使用靜電補償法來測G,實驗原理如圖(b)所示。通過吸引質量產生的引力力矩和伺服反饋電壓產生的力矩平衡,他們1995年公布的實驗結果為。1999年,他們公布的改進實驗結果為[72](MSL-99)。此後的進一步改進實驗給出[45](MSL-03),相對不確定度達到40ppm。DeBoer[9]在1987年嘗試著用水銀的浮力來支撐檢驗質量,並且利用靜電補償平衡引力矩,得到的G值為。1995年,Michaelis等人[73]用原理基本相同的方法重新測量了萬有引力常數,得到的結果為(PTB-95)。該結果比後來其他實驗結果均偏大很多,而且在他們的後期研究中也發現該實驗中存在無法確定的系統誤差[74],因此在CODATA-02基本物理常數調整時,該結果沒有被採納。