質點在有心力場中的運動
有心力對其力心的矩為零,根據動量矩定理,質點對力心的動量矩是常矢量,因此,運動軌道是平面曲線。此時,用極坐標描述質點在有心力場中的運動比較方便。若以 Ox(圖1)作為參考線,只受有心力作用的質點 Q的極坐標為:
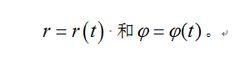 有心力場
有心力場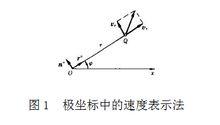 有心力場
有心力場如將 Q點的運動分解為矢徑繞 O轉動的牽連運動和質點沿轉動矢徑的相對運動和,可得到:
徑向速度
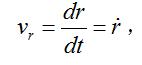 有心力場
有心力場橫向速度
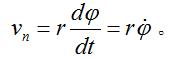 有心力場
有心力場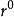 有心力場
有心力場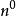 有心力場
有心力場如以 和 分別表示徑向和橫向單位矢量,則 Q點的速度矢量可寫為:
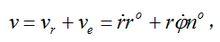 有心力場
有心力場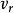 有心力場
有心力場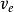 有心力場
有心力場式中 和 分別為 Q點的相對速度和牽連速度。
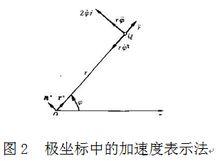
Q點的加速度由三部分組成(圖2):
相對加速度
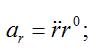 有心力場
有心力場牽連加速度
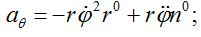 有心力場
有心力場科里奧利加速度
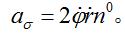 有心力場
有心力場因此,質點 Q的加速度可分解為徑向和橫向兩部分:
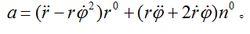 有心力場
有心力場 有心力場
有心力場質點只受有心力作用時,其矢量在平面上單位時間掃過的面積稱為面積速度。設 為面積速度, r為質點的矢徑, v為質點的速度,則
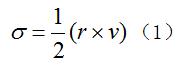 有心力場
有心力場 有心力場
有心力場 有心力場
有心力場式中 垂直於 r和 v所成的平面。另外, 還可寫為:
 有心力場
有心力場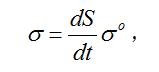 有心力場
有心力場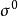 有心力場
有心力場 有心力場
有心力場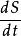 有心力場
有心力場式中為沿的單位矢量;為面積速度值。由於
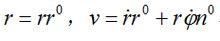 有心力場
有心力場代入式(1)後得:
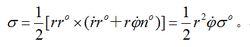 有心力場
有心力場因而面積速度值為:
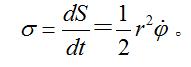 有心力場
有心力場質點在有心力場中運動時,滿足面積定律:質點在有心力場中運動時,矢徑掃過的面積速度守恆。克卜勒從行星運動的觀察記錄中得到這一經驗規律,稱為克卜勒第二定律(見開普靭定律);但此定律並不只適用於平方反比律的力,而且適用於有心力運動的一般情況。從有心力場中運動質點對力心的動量矩守恆,即
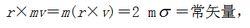 有心力場
有心力場 有心力場
有心力場得到=常矢量,因而
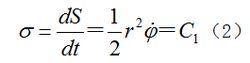 有心力場
有心力場或寫為:
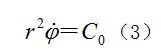 有心力場
有心力場積分式(2),得到:
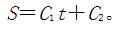 有心力場
有心力場這就是面積定律的數學表示式。
若質點 Q在有心力場中運動(圖3)。將 ma= F在矢徑上投影,因 F沿徑向,故有:
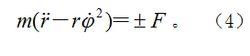 有心力場
有心力場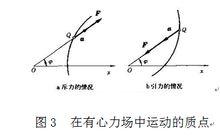 有心力場
有心力場這就是以極坐標表示的有心力場中質點的運動微分方程,式中正號表示斥力的情況;負號表示引力的情況。牛頓萬有引力場具有引力的特性,而在庫侖靜電場中吸引和排斥都有可能。
 有心力場
有心力場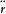 有心力場
有心力場如令式(3)中的 r=1/μ,則可將、寫作:
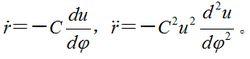 有心力場
有心力場 有心力場
有心力場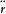 有心力場
有心力場把和代入式(4)後,即得出比奈公式:
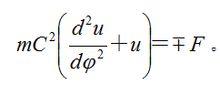 有心力場
有心力場利用這個公式,可從質點運行的軌道決定它所受的力;反之,也可從質點所受的有心力決定它的軌道。
參考文獻
1、詞條作者:黃克累.《中國大百科全書》74卷(第一版)力學 詞條:有心力場:中國大百科全書出版社,1987 :562-563頁.

