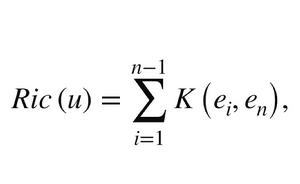簡介
 里奇曲率
里奇曲率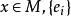 里奇曲率
里奇曲率 里奇曲率
里奇曲率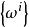 里奇曲率
里奇曲率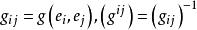 里奇曲率
里奇曲率設(M,g)為 維黎曼流形,R為黎曼曲率張量, 為 點處的任意一個切標架,對偶的餘切標架是 。設 ,則里奇曲率張量(Ricci curvature tensor) 是
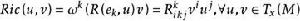 里奇曲率
里奇曲率對於任意非零切向量u,稱
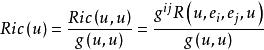 里奇曲率
里奇曲率 里奇曲率
里奇曲率為在 點沿切方向u的里奇曲率。
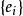 里奇曲率
里奇曲率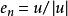 里奇曲率
里奇曲率若取 為單位正交切標架,且 ,則易知
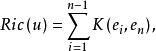 里奇曲率
里奇曲率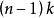 里奇曲率
里奇曲率即里奇曲率是n-1個截面曲率的和,因此關於里奇曲率為正或負的假定弱於關於截面曲率為正或負的假定。特別地,若M具有常截面曲率k,則M的里奇曲率為 。
相關概念
數量曲率
[scalar curvature]
 里奇曲率
里奇曲率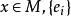 里奇曲率
里奇曲率 里奇曲率
里奇曲率設(M,g)為 維黎曼流形, 為 點處的單位正交切標架。則稱
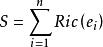 里奇曲率
里奇曲率 里奇曲率
里奇曲率為在點 處的數量曲率。
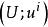 里奇曲率
里奇曲率在局部坐標系 下,數量曲率 S 的表達式為
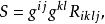 里奇曲率
里奇曲率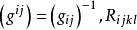 里奇曲率
里奇曲率式中, 為黎曼曲率張量R在該局部坐標系下的分量。
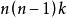 里奇曲率
里奇曲率特別地,若 M 具有常截面曲率k,則 M 的數量為 。
截面曲率
[sectional curvature]
截面曲率是曲面內蘊幾何學中高斯曲率在黎曼幾何中的推廣。
 里奇曲率
里奇曲率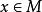 里奇曲率
里奇曲率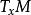 里奇曲率
里奇曲率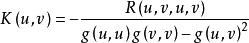 里奇曲率
里奇曲率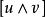 里奇曲率
里奇曲率設(M,g)為 維黎曼流形,R為黎曼曲率張量。 ,對於 中的任意兩個線性無關的向量u、v,稱 為在點沿截面 截面曲率。
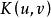 里奇曲率
里奇曲率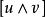 里奇曲率
里奇曲率 里奇曲率
里奇曲率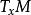 里奇曲率
里奇曲率證明 的值只依賴於二維截面 (即 M 在點 的切空間 的一個二維子空間),而與該截面的基底 u,v 的選取無關。
截面曲率是黎曼幾何中重要的內蘊幾何量,它反映了空間彎曲的程度,並在曲線弧長的第二分公式中自然地出現,它為正成負,影響了該空間中測地線的大範圍性狀。