簡介
曲率張量可指黎曼曲率張量或者里奇曲率張量。
黎曼曲率張量
 曲率張量
曲率張量 在微分幾何中, 黎曼曲率張量或 黎曼張量是表達黎曼流形的曲率的標準方式,更普遍的,它可以表示有仿射聯絡的流形的曲率 ,包括無扭率或有撓率的。曲率張量通過列維-奇維塔聯絡(更一般的,一個仿射聯絡) (或者叫協變導數)由下式給出:
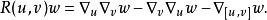 曲率張量
曲率張量 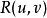 曲率張量
曲率張量 這裡 是一個流形切空間的線性變換;它對於每個參數都是線性的。
注意有些作者用相反的符號定義曲率.
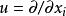 曲率張量
曲率張量 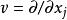 曲率張量
曲率張量 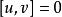 曲率張量
曲率張量 如果 與 是坐標向量場則 所以公式簡化為
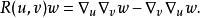 曲率張量
曲率張量 也就是說曲率張量衡量 協變導數的反交換性。
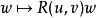 曲率張量
曲率張量 線性變換 也稱 曲率變換。
對稱性和恆等式
進一步,由上式定義了如下的三重線性映射
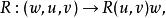 曲率張量
曲率張量 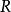 曲率張量
曲率張量 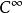 曲率張量
曲率張量 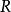 曲率張量
曲率張量 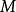 曲率張量
曲率張量 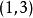 曲率張量
曲率張量 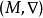 曲率張量
曲率張量 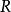 曲率張量
曲率張量 映射 關於每一個自變數都是 線性的, 故 是 上的 型光滑張量場, 稱之為紡射聯絡空間 的曲率張量. 在坐標向量場下, 可以表示為
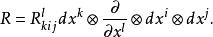 曲率張量
曲率張量 還可以定義四重線性映射,如下
 曲率張量
曲率張量 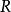 曲率張量
曲率張量 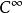 曲率張量
曲率張量 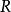 曲率張量
曲率張量 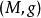 曲率張量
曲率張量 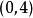 曲率張量
曲率張量 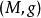 曲率張量
曲率張量 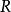 曲率張量
曲率張量 則映射 關於每一個自變數都是 線性的, 故 是黎曼流形 上的 型光滑張量場, 稱之為黎曼流形 的黎曼曲率張量. 在坐標向量場下, 可以表示為
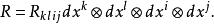 曲率張量
曲率張量 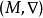 曲率張量
曲率張量 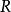 曲率張量
曲率張量 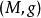 曲率張量
曲率張量 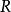 曲率張量
曲率張量 註:上述紡射聯絡空間 上的曲率張量 與黎曼流形 上的黎曼曲率張量 是同一個對象的不同表現形式.
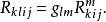 曲率張量
曲率張量 注
黎曼曲率張量有如下的對稱性:
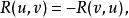 曲率張量
曲率張量 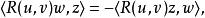 曲率張量
曲率張量 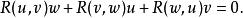 曲率張量
曲率張量 最後一個恆等式由里奇(Ricci)發現,但是稱為 第一比安基恆等式(First Bianchi identity)或 代數比安基恆等式(Algebraic Bianchi identity),因為和下面的比安基恆等式相像 。
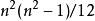 曲率張量
曲率張量 這三個恆等式組成曲率張量對稱性的完整列表,也就是給定說任何滿足上述恆等式的張量,可以找到一個黎曼流形在某點的曲率張量和它一樣。簡單的計算表明這樣一個張量有 個獨立分量。
另一個有用的恆等式可以由上面這些導出:
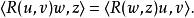 曲率張量
曲率張量 比安基恆等式(Bianchi identity),經常也叫 第二比安基恆等式(Second Bianchi identity)或 微分比安基恆等式(Differential Bianchi identity)。它涉及到協變導數:
 曲率張量
曲率張量 給定流形某點的任一坐標表示,上述恆等式可以用黎曼曲率張量的分量形式表示為:
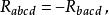 曲率張量
曲率張量 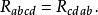 曲率張量
曲率張量 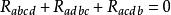 曲率張量
曲率張量 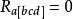 曲率張量
曲率張量 第一(代數)比安基恆等式: 或等價地寫為
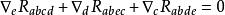 曲率張量
曲率張量 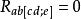 曲率張量
曲率張量 第二(微分)比安基恆等式: 或等價地寫為
其中方括弧表示對下標的反對稱化,分號表示協變導數。這些恆等式在物理中有套用,特別是廣義相對論。
里奇曲率張量
在微分幾何中,類似度量張量,里奇張量也是一個在黎曼流形每點的切空間上的對稱雙線性形式。以格雷戈里奧·里奇-庫爾巴斯托羅(Gregorio Ricci-Curbastro)為名的 里奇張量或 里奇曲率張量(Ricci curvature tensor)。提供了一個數據去描述給定的黎曼度規(Riemannian metric)所決定的體積究竟偏離尋常歐幾里得 n-空間多少的程度。粗略地講,里奇張量是用來描述“體積扭曲”的一個值;也就是說,它指出了 n-維流形中給定區域之 n-維體積,其和歐幾里得 n-空間中與其相當之區域的體積差異程度。更精確的描述請見下文“直接的幾何意義”段落 。
正式定義
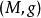 曲率張量
曲率張量 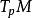 曲率張量
曲率張量 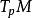 曲率張量
曲率張量 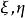 曲率張量
曲率張量 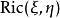 曲率張量
曲率張量 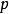 曲率張量
曲率張量 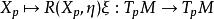 曲率張量
曲率張量 設 是一個 n-維黎曼流形。 記 為 M在 p點的切空間, 任給切空間 中的一對向量 ,Ricci 張量 在 點的值定義為線性映射 的跡(trace),也就是說:
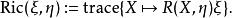 曲率張量
曲率張量 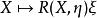 曲率張量
曲率張量 右手邊 R是所謂黎曼曲率張量,而 是切空間之間的線性映射,所以可以計算這映射的跡。在局部坐標系下有
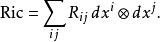 曲率張量
曲率張量 使用愛因斯坦求和約定的話,上式會寫成:
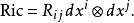 曲率張量
曲率張量 其中,
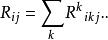 曲率張量
曲率張量 注意,之後的方程如果使用愛因斯坦求和約定,不會特別註明。
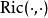 曲率張量
曲率張量  曲率張量
曲率張量 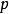 曲率張量
曲率張量 已經知道里奇張量 ,如今就可以用里奇張量來定義里奇曲率。如果 為 點的單位向量,則
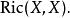 曲率張量
曲率張量 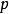 曲率張量
曲率張量  曲率張量
曲率張量 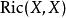 曲率張量
曲率張量 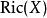 曲率張量
曲率張量 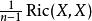 曲率張量
曲率張量 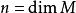 曲率張量
曲率張量 定義為在點 , 方向的里奇曲率,有時會把 寫成 。也有些人會定義里奇曲率為 這裡 。
直接的幾何意義
對於黎曼流形(M,g)里任意一點p的旁邊可以定義被稱為測地法座標系的局部座標系。這些通過p的測地線不但都對應著通過原點的直線,而且同時構成了從p的距離和從原點的歐幾里得距離的對應。這個座標系的度量張量是
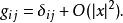 曲率張量
曲率張量 好處就是,此座標是歐幾里得度量的良好近似。實際上,由於在法座標系的放射測地線產生的雅可比場適用的度量的泰勒展開,
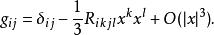 曲率張量
曲率張量 可以得到
然後,在這個座標系,在p可以得到以下體積元素的展開。
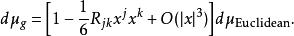 曲率張量
曲率張量 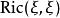 曲率張量
曲率張量 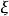 曲率張量
曲率張量 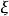 曲率張量
曲率張量 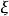 曲率張量
曲率張量 然後,如果里奇曲率 在向量 的方向是正的,由於在M上從p向 方向的短的測地線收束族掃過的圓錐區域的體積比在歐幾里得空間對應的圓錐區域要小。如此類推,如果里奇曲率在給定的向量 的方向是負的,流形同樣的圓錐區域的體積比歐幾里得空間對應的圓錐區域要大。
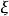 曲率張量
曲率張量  曲率張量
曲率張量 里奇曲率本質上就是包含 的平面的曲率平均。也就是說最初是圓形(或者是球形)放射狀的圓錐會扭曲未橢圓形狀,沿著主軸的彎曲是相互相反的作用,而且有把體積變為零的可能性。然后里奇曲率沿著 會變為零。在物理的套用,一定要變零的切斷曲率的存在並不一定是局部性一定有什麼質量。世界線圓錐最初的圓形的橫切面是,要是變成了後來體積沒變化的橢圓,這個效果就是來自其他位置的質量的潮汐效果 。
無跡的里奇張量
在黎曼幾何與廣義相對論中,一個偽黎曼流形(pseudo-Riemannian manifold){\displaystyle (M,g)}之 無跡的里奇張量(trace-free Ricci tensor)是一個定義如下的張量
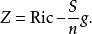 曲率張量
曲率張量 