概念
酉幾何(unitary geometry)是一種向量空間的幾何。即關於非退化埃爾米特型H的有限維向量空間的研究。設基域為含q 個元的有限域F ,其中有一個2階自同構a→a'=a ,它的固定子域為F。對任意向量x,y,z及F 中任意元a,b,這裡的埃爾米特型由以下兩式定義:
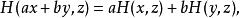 酉幾何
酉幾何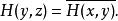 酉幾何
酉幾何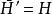 酉幾何
酉幾何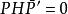 酉幾何
酉幾何對取定的一組基{e,e,…,e},埃爾米特型H的矩陣H=(H(e,e))滿足,即為埃爾米特矩陣。設P是V(F )的m維子空間,代表子空間P的秩為m的m×n矩陣仍用P表示。設H是非奇異埃爾米特矩陣,若,則稱P為全迷向子空間;若PH非奇異,則稱P為非迷向子空間。利用酉空間中不同類型的子空間,可以構作PBIBD設計及BIBD設計。例如,取有限域F 上3維酉幾何中1維迷向子空間的全體作為處理的集合,並取其中2維非迷向子空間的全體作為區組的集合,規定關聯關係為子空間之間的包含關係,於是,由此得到一個(q +1,q+1,1)-BIBD。
向量空間
設K為交換體。稱賦以由下列兩個給定法則所定義的代數結構的集合E為K上的向量空間:
——記為加法的合成法則,
 酉幾何
酉幾何——記為乘法的作用法則,即從K×E到E中的映射,
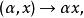 酉幾何
酉幾何這兩個法則滿足下列條件:
a)賦以加法的集合E是交換群;
b) 對K的任一元素偶(α,β),以及對E的任一元素x,
α(βx)=(αβ)x;
c) 對E的任一向量x,1x=x,其中1表示體K的單位元素;
d)對K的任一元素偶(α,β),以及對E的任一元素偶(x,y),
(α+β)x=αx+βx
α(x+y)=αx+αy.
當體K不再假定為交換的時,滿足上述條件的集合E稱為K上的左向量空間;
如果條件α(βx)=(αβ)x換為α(βx)=(βα)x,則稱E為K上的右向量空間。在這種情況下,E上的作用法則記為:
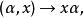 酉幾何
酉幾何例如,設K為交換體,而E為只有一個記為0的元素的集合. E賦以兩個法則:(0,0)↦0,(α, 0)↦0,則E為K上的向量空間。
迷向子空間
一種子空間。給定子空間按埃爾米特函式的正交子空間。設φ是域P上的線性空間V的埃爾米特函式。對埃爾米特函式而言,左、右正交是一致的。因此,若V中向量α,β的內積(α,β)=0,則稱α與β正交。設M是V的子空間,若M ={α∈V|β∈M,φ(α,β)=0},則M 是V的子空間,稱為M的正交補(空間)。若M∩M≠0,則稱子空間M是迷向的;此時有非零向量α∈M使(α,α)=0,α稱為非零迷向向量。若MM,則稱M為全迷向子空間。若V為有限維線性空間,φ為非退化埃爾米特函式,則V=M⊕M ,這時M與M 的維數有關係:
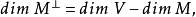 酉幾何
酉幾何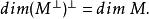 酉幾何
酉幾何酉代數
具有單位元的數學結構稱為酉數學結構.酉代數,即是對於乘法有單位元的結合代數。酉代數E的子代數稱為酉子代數,如果它含有E的單位元素。
例如,向量空間的全體自同態之代數是酉代數。但是,全體在R上連續且在無窮遠處趨於零的復值函式之代數不是酉代數。
自同態
指從群胚,么半群,群,環到其自身中的同態,向量空間在自身中的線性映射,等等。
設G為關於加法的交換群。賦以加法及法則(f,g)↦g°f的G的全體自同態之集是一個環。
設E為交換體K上的向量空間。賦以法則(f, g)↦g°f, E的全體自同態之向量空間是酉代數,記為ℒ(E),或End(E)。元素g°f仍記為gf。A-模的情形是類似的。
人物簡介——埃爾米特
法國數學家。生於洛林(Lorraine)地區的迪約茲(Dieuze),卒於巴黎。1842年進入巴黎理工科大學學習。由於先天性的右腿殘疾,他曾遭受到一些人的歧視,但是,不久,他就以對橢圓函式諸問題的深入研究,贏得了著名數學家雅可比的賞識。1848年擔任了巴黎理工科大學的輔導教師,1856年被選為巴黎科學院院士,1869年成為理工科大學分析學教授,並受聘為巴黎大學的高等代數教授。他還是彼得堡科學院的名譽院士。埃爾米特在特殊函式論、數論、高等代數、數學分析等許多方面都做了很有價值的工作。他研究了橢圓函式和阿貝爾函式的除法和變換,並套用橢圓函式解5次方程,解決了包含這種函式的力學問題。他推廣了高斯研究整係數有限二次型的方法,證明了它們對任意個變數其類數仍是有限的;深入考查了矩陣理論,證明了若矩陣M=M*,則其特徵根為實數。他還研究了正交多項式中的一類,即所謂埃爾米特多項式,又稱切比雪夫多項式;分析了多項式族與多變數的相似性,研究了整數用代數形表示的問題;引入了復二次型,稱為埃爾米特型,特別是在1873年證明了數e的超越性,這是很有名的結果。
