定義
酉運算元又叫保范運算元,它是歐式空間中旋轉概念在無窮維情況下的推廣;希爾伯特空間的酉運算元是仍保持其內積意義的希爾伯特空間的線性變換。酉運算元具有逆運算元,其逆運算元也是一種酉運算元,且酉運算元和其逆運算元是一對共軛運算元。酉變換是泛函分析和運算元理論中的一個重要概念,傅立葉變換就是酉變換之一例。
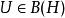 酉運算元
酉運算元設,若滿足:
 酉運算元
酉運算元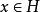 酉運算元
酉運算元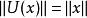 酉運算元
酉運算元(1)是等距的,即對任意,都有;
 酉運算元
酉運算元(2)是滿射。
 酉運算元
酉運算元則稱為酉運算元。
各種條件
充要條件
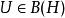 酉運算元
酉運算元 酉運算元
酉運算元設,則為酉運算元等價於:
 酉運算元
酉運算元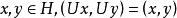 酉運算元
酉運算元(1)是滿射且對任意;
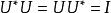 酉運算元
酉運算元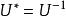 酉運算元
酉運算元(2),即。
證明:
(1)充分性顯然成立,下面證明必要性。
 酉運算元
酉運算元 酉運算元
酉運算元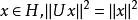 酉運算元
酉運算元設為酉運算元,即是滿射且等距的,對任意,由極化恆等式得到下述等式:
 酉運算元
酉運算元當是實空間時,有:
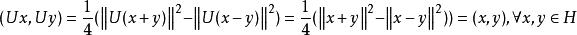 酉運算元
酉運算元 酉運算元
酉運算元當是復空間時,有:
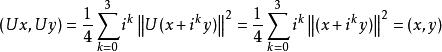 酉運算元
酉運算元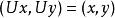 酉運算元
酉運算元故有。
(2)首先來證必要性。
 酉運算元
酉運算元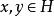 酉運算元
酉運算元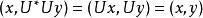 酉運算元
酉運算元設為酉運算元,由(1)得,對任意的,有:,
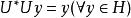 酉運算元
酉運算元所以得:;
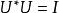 酉運算元
酉運算元故有:。
 酉運算元
酉運算元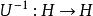 酉運算元
酉運算元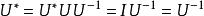 酉運算元
酉運算元因此是單射,因而 存在,且有:。
下面來證充分性。
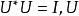 酉運算元
酉運算元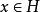 酉運算元
酉運算元由等式為滿射,且對,有:
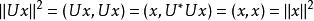 酉運算元
酉運算元 酉運算元
酉運算元故為酉運算元。證畢。
必要條件
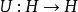 酉運算元
酉運算元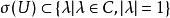 酉運算元
酉運算元設為酉運算元,則,即酉運算元的譜都在單位圓上。
酉運算元的等價形式
預備知識
在複變函數中,保角映射在理論和套用上都十分重要,而具有保角性和伸縮率不變性的映射即為保角映射,將此概念推廣到無窮維空間,特給出如下定義:
 酉運算元
酉運算元設為線性運算元,
 酉運算元
酉運算元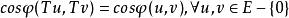 酉運算元
酉運算元 酉運算元
酉運算元(1)若運算元滿足,則稱運算元為保角運算元;
 酉運算元
酉運算元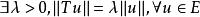 酉運算元
酉運算元 酉運算元
酉運算元(2)若運算元滿足,則稱運算元為相似運算元;
 酉運算元
酉運算元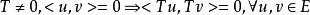 酉運算元
酉運算元 酉運算元
酉運算元(3)若運算元滿足,則稱運算元為第一型保正交運算元;
 酉運算元
酉運算元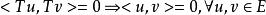 酉運算元
酉運算元 酉運算元
酉運算元(4)若運算元滿足,則稱運算元為第二型保正交運算元;
 酉運算元
酉運算元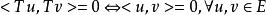 酉運算元
酉運算元 酉運算元
酉運算元(5)若運算元滿足,則稱運算元為正交不變運算元;
 酉運算元
酉運算元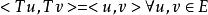 酉運算元
酉運算元 酉運算元
酉運算元(6)若運算元滿足,則稱運算元為酉運算元,或保內積運算元。
定理內容
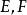 酉運算元
酉運算元 酉運算元
酉運算元 酉運算元
酉運算元 酉運算元
酉運算元 酉運算元
酉運算元設為Hilbert空間,為由到的線性運算元,則關於運算元的如下六個命題為等價命題:
 酉運算元
酉運算元(1)為保角運算元;
 酉運算元
酉運算元(2)為相似運算元;
 酉運算元
酉運算元(3)為第一型保正交運算元;
 酉運算元
酉運算元(4)為第二型保正交運算元;
 酉運算元
酉運算元(5)為正交不變運算元;
 酉運算元
酉運算元(6)為酉運算元。

