簡介
如果方程要求未知量y(x)及其導數y′(x)在自變數的同一點x=x取給定的值,即y(x )=y,y′(x)= y′,則這種條件就稱為初始條件,由方程和初始條件構成的問題就稱為初值問題;
而在許多實際問題中,往往要求微分方程的解在某個給定區間a ≤ x ≤b的端點滿足一定的條件,如y(a) = A , y(b) = B,則給出的在端點(邊界點)的值的條件,稱為邊界條件,微分方程和邊界條件構成數學模型就稱為邊值問題。
分類
邊值問題中的邊界條件的形式多種多樣,在端點處大體上可以寫成這樣的形式,Ay+By'=C,若B=0,A≠0,則稱為第一類邊界條件或狄里克萊(Dirichlet)條件;B≠0,A=0,稱為第二類邊界條件或諾依曼(Neumann)條件;A≠0,B≠0,則稱為第三類邊界條件或洛平(Robin)條件。
總體來說,
第一類邊界條件:
給出未知函式在邊界上的數值;
第二類邊界條件:
給出未知函式在邊界外法線的方嚮導數;
第三類邊界條件:
給出未知函式在邊界上的函式值和外法線的方嚮導數的線性組合。
對應於comsol,只有兩種邊界條件:
Dirichlet boundary(第一類邊界條件)—在端點,待求變數的值被指定。
Neumann boundary(第二類邊界條件)—待求變數邊界外法線的方嚮導數被指定。
再補充點初始條件:
初始條件,是指過程發生的初始狀態,也就是未知函式及其對時間的各階偏導數在初始時刻t=0的值.在有限元中,好多初始條件要預先給定的。不同的場方程對應不同的初始條件。
總之,為了確定泛定方程的解,就必須提供足夠的初始條件和邊界條件!
爆破技術
我國高等級公路經過近二十年的建設取得了巨大成就,高等級公路里程迅速增加。高等級公路建設逐漸由平原微丘區向山嶺重丘區延伸發展。尤其是隨著西部大開發戰略的實施,西部公路建設所面臨的地質地形將會越來越多的遇到起伏不平的岩石山區。為了滿足高等級公路所需的技術標準,必須克服波浪起伏、高差較大、溝谷相間等各種不利地形,深挖高填土石方工程難以避免。而深挖高填工程數量大、傳統施工速度慢、施工效率低下,同橋遂工程一樣,往往成為決定工程進度的關鍵。因此,必須研究推廣採用新的爆破技術,以在山區高等級公路建設中加快石方路基工程的施工進度並確保施工質量。
多邊界條件下爆破技術
隨著鑿岩機具、裝運機具和爆破技術的發展,基於多邊界條件爆破理論對公路工程影響較大的爆破技術是光面爆破和預裂爆破、深孔爆破以及微差爆破技術。
1.1多邊界條件爆破
多邊界條件即為地形變化條件,一般分為平坦地形、傾斜地形、山包地形和埡口地形。多邊界爆破遵循“最小抵抗線原理”。多邊界藥量計算如下。
Q=edKW3F(E·α)
式中Q———為藥包的裝藥量,kg;
e———為炸藥換算係數;d———為堵塞係數;
K———形成標準拋擲漏斗時的線耗藥量,kg/m3;
W———為最小抵抗線,m;F———(E,α)為藥包性質指數;E———為拋擲(坍)率(%);
α———為自然地面坡度(°)。
多邊界條件下的爆破漏斗示意藥包間距(m):a=(1.0~1.2)W子藥包間距(m)
C=0.5nWsinα+1
式中W———為相鄰兩藥包最小抵抗線的平均值;
n———為爆破作用指數,其餘同前。爆破作用半徑:
下爆破作用半徑R下=Wn2+1
上爆破作用半徑R上=WAa上n2+1式中a上———為抵抗線出口點至上破壞點之間的地
面坡度,(°);A———為崩塌係數。
1.2光面爆破和預裂爆破
光面爆破和預裂爆破是專門針對設計開挖界面進行有效控制的爆破方法。沿爆破開挖區的設計輪廓或邊坡,以較小的間距合理布置一排相互平行的鑽孔,在孔內採用間歇或不耦合裝藥,並在開挖區主爆破之後或之前同時起爆,從而獲得符合設計輪廓、光滑平整和穩定性好的邊坡面。
光面爆破和預裂爆破在技術上採用室洞控制爆破方法,其核心是藥包布置原則。包括:
(1)在任何情況下,藥包布置均以最小抵抗線為設計依據;
(2)根據路塹中心挖深和寬度,進行藥包分層布置;
(3)儘量對藥包進行縱向或橫向分集或分條布置;
(4)合理安排藥包的起爆時間。光面爆破和預裂爆破的主要參數有鑽
孔直徑、孔間距、抵抗線、線裝藥量、裝藥結構、最後一排主爆孔與裂孔間距等。
鑽孔直徑(d):一般以50mm~70mm為宜,為增加不耦合係數也可採用100mm~150mm。另外,孔深較大也可用較大的鑽孔直徑。
炮孔間距(a):孔距與孔徑成正比例關係,並與岩性、岩體構造和炸藥類型等因素有關,即a=mαd。對於預裂爆破md=10~12;光面爆破md=10~16。同時在光面爆破中孔距與最小抵抗線W成正比,即a=mW,一般m處於0.6~1.0之間。
線裝藥量q(kg/m);光面爆破q=(0.1~0.15)KaW;預裂爆破q=(0.1~0.4)Ka2 式中符號同前。
裝藥結構既能滿足設計規定的不耦合係數值,又要儘可能保證藥包爆炸後,爆能沿鑽孔全長均勻分布。裝藥結構一般有連續裝藥和間隔裝藥兩種。
1.3深孔爆破
深孔爆破就是炮孔孔徑大於75mm且深度在5m以上的採用延長藥包的一種爆破方法,通常有拉槽深孔爆破和台階深孔爆破兩種。炮孔需用大型的潛孔鑿岩機或穿孔機鑽空。當用機械清方時,採用台階深孔爆破效果更好,可以實現路基石方施工全面機械化。
深孔爆破的優點是勞動生產率高,一次爆落的方量多,施工進度快,爆破時對路基邊坡的影響比大炮小。若配合預裂或光面爆破,則邊坡穩定,爆破效果易控制,爆破時比較安全。但由於需用大型機械,故轉移工地、開闢場地、修築便道等準備工作都比較複雜,且爆破後仍有10%~25%的大石塊需經第二次爆破解小。
深孔爆破梯段傾角最好為60°~75°,高度應在5m~15m之間。可採用垂直孔和斜孔兩種炮孔,孔徑通常為80mm~300mm。公路工程中以100mm~150mm為宜。超鑽長度大致是梯段高度的10%~15%。岩石堅硬者取大值。
垂直孔深度(m):l=H+h斜孔的深度(m):l=H+h炮孔的間距(m):a=MW
底板抵抗線(m):W=D7.85ptl
KmH式中m———約為0.6~1.4,常取0.7~0.85;
D———為鑽空直徑,dm;p———為炸藥密度,kg/m3;K———為單位耗藥量,kg/m3,且K′=K/3;τ———為深孔裝藥係數;
H———為梯段高度,m;其餘同前。
當H<10m時,τ=0.6;H=10m~15m時;τ=0.5;H=15m~20m時,τ=0.4。W值確定後按下式估算L值:
L=W-H·cotα式中L———為炮孔與梯段頂邊緣的距離,m;
其餘同前。為確保鑿岩機作業安全,此值應大於2m~3m;否則,需調整W值。
多排孔時,排的間距b可取b=W。最後按下式計算炸藥量Q(kg):
Q=eK′WHa式中符號同前。
1.4微差爆破
多發一次爆破採用微差爆破技術具有減震、前發藥包為後發藥包開創凌空面進而加強岩石破碎效果、降低一次爆破堆積高度、有利於機械作業、減少岩石夾制力、節省炸藥、並可增大孔距等優點,提高每百米的炸落方量。
1.5拋擲(坍)爆破定向爆破和鬆動爆破
對於自然坡度較陡(>30°),地形地質條件較為複雜、凌空面大時,採用拋坍爆破。拋坍爆破利用岩石本身的自重坍滑出路基,提高爆破效果,從而加快施工進度並降低工程造價。當路線通過波浪起伏的峽谷或雞爪地形地段、橫切山包或山嘴、凌空面較多時,採用拋坍或拋擲爆破效率更為顯著。
在以借為填或移挖作填地段,特別是深挖高填相間、工程量大的雞爪型地區,採用定向爆破,一次可形成百米以上至數百米路基。
在軟石、次堅石路基地段,採用鬆動爆破技術,配合機械化施工作業,可大大提高施工效率,在堅石路段宜採用深孔技術進行鬆動爆破。
路基石方特點
2.1工程數量大,占路基土石方工程數量比例也大。個別路段每公里可高達十多萬立方米,占路段土石方總量的95%以上,占整段公路投資的65%以上。有必要進行爆破施工和機械化作業。
2.2石方工程相對集中。有利於大爆破施工和機械化作業。
2.3地形地質相對複雜,地形緩陡連續或相間、地勢迂迴曲折;地質岩石也可能呈現為軟石、次堅石、堅石連續或相間。需要採用各種爆破技術綜合爆破,且裝運推機械進場有一定困難。
3公路石方路基施工探討
通常將邊坡高度等於或大於20m的石質路塹稱為深挖石方路塹。其挖深較大、石方集中、地形複雜、施工難度大。公路部門傳統石方機械化水平較底,爆破施工隊伍技術力量較薄弱,同時受地形和地質條件制約,深挖石方路塹施工方法主要是採用淺眼爆破、藥壺炮、貓洞炮和普通洞室炮爆破進行。存在以下缺點。
3.1淺眼爆破、藥壺炮、貓洞炮等小炮開挖方法因受岩石地質條件、
機械清方等因素影響較大,爆破工效低,施工速度慢,同時在地質條件不好的情況下未必能形成高大而美觀的岩石邊坡;
3.2普通洞室爆破因其技術含量低,對岩石邊坡、周圍環境都會產生較大的破壞;
3.3加大鑿岩設備投入、克服地形條件制約,在深挖石方路塹的施工中儘量使用中深孔爆破,確保快速、優質的工程效果,這一做法目前尚未達成共識。因此,採用控制爆破技術,改變人們落後的爆破施工意識,探討深挖石方路塹的快速優質施工技術,是山區高等級公路施工中亟待解決的問題。根據多邊界爆破理論在209國道和318國道恩施州改建
結語
公路石方爆破施工是一項技術含量高的綜合性工作,必須提高認識,根據路段地形地質、施工機具及工程整體安排等條件進行合理設計和組織施工,對加快工程進度、保證工程質量和施工安全都具有重要的意義。
因此,根據工程實踐總結積累經驗,推廣新的爆破技術和施工方法是山區高等級公路修建的一項重要任務。
施工方法
(1)正確確定周邊炮眼的位置、
方向、深度、角度,並選用低密度、低爆速和高體積威力的炸藥,是保證光面爆破成功和增強爆破效果的關鍵。
(2)採用預留邊坡保護層、分集或分條分層布置藥包、鬆動或拋坍洞室控制爆破進行路塹主體方量開挖,然後至坡頂向下用挖掘機配合淺眼爆破進行刷坡和清方,能適用於各種複雜地形條件的深挖石方路塹開挖,且成本低廉。
(3)採用預裂———洞室控制爆破相結合的方法進行深路塹石方深孔爆破或鬆動爆破方快速開挖,然後用挖掘機、推土機、裝載機配合自卸氣車聯合清方,效果更為顯著。
(4)利用有利地形進行定向爆破、拋坍(擲)業,對具有一定岩石厚度邊坡路塹具有顯著效果。
軟體測試
計算機邊界條件
邊界條件是指軟體計畫的操作界限所在的邊緣條件.如果軟體測試問題包含確定的邊界,那么數據類型可能是:
數值速度字元地址位置尺寸數量,同時,考慮這些類型的下述特徵:
第一個/最後一個最小值/最大值
開始/完成超過/在內
空/滿最短/最長
最慢/最快最早/最遲
最大/最小最高/最低
相鄰/最遠
越界測試
方法
通常是簡單加1或者很小的數(對於最大值)和減少1或者很小的數(對於最小值),例如:
第一個減1/最後一個加1
開始減1/完成加1
空了再減/滿了再加
慢上加慢/快上加快
最大數加1/最小數減1
最小值減1/最大值加1
剛好超過/剛好在內
短了再短/長了再長
早了更早/晚了更晚
最高加1/最低減1
另一些該注意的輸入:默認,空白,空值,零值和無;非法,錯誤,不正確和垃圾數據。
選用原則
一、如果輸入條件規定了值的範圍,則應該取剛達到這個範圍的邊界值,以及剛剛超過這個範圍邊界的值作為測試輸入數據;
二、如果輸入條件規定了值的個數,則用最大個數、最小個數、比最大個數多1格、比最小個數少1個的數做為測試數據;
三、根據規格說明的每一個輸出條件,使用規則一;
四、根據規格說明的每一個輸出條件,使用規則二;
五、如果程式的規格說明給出的輸入域或輸出域是有序集合(如有序表、順序檔案等),則應選取集合的第一個和最後一個元素作為測試用例;
六、如果程式用了一個內部結構,應該選取這個內部數據結構的邊界值作為測試用例;
七、分析規格說明,找出其他可能的邊界條件。
值法舉例
找零錢最佳組合
假設商店貨品價格(R)皆不大於100元(且為整數),若顧客付款在100元內(P),求找給顧客之最少貨幣個(張)數?(貨幣面值50元(N50),10元(N10),5元(N5),1元(N1)四種)
一、分析輸入的情形。
R>100
0<R<=100
R<=0
P>100
R<=P<=100
P<R
二、分析輸出情形。
N50=1
N50=0
4>N10>=1
N10=0
N5=1
N5=0
4>N1>=1
N1=0
三、分析規格中每一決策點之情形,以RR1,RR2,RR3表示計算要找50,10,5元貨幣數時之剩餘金額。R>100R<=0
P>100
P<R
RR1>=50
RR2>=10
RR3>=5
四、由上述之輸入/輸出條件組合出可能的情形。
R>100
R<=0
0<R<=100,P>100
0<R<=100,P<R
0<R<=100,R<=P<=100,RR=50
0<R<=100,R<=P<=100,RR=49
0<R<=100,R<=P<=100,RR=10
0<R<=100,R<=P<=100,RR=9
0<R<=100,R<=P<=100,RR=5
0<R<=100,R<=P<=100,RR=4
0<R<=100,R<=P<=100,RR=1
0<R<=100,R<=P<=100,RR=0
五、為滿足以上之各種情形,測試資料設計如下:
1.貨品價格=101
2.貨品價格=0
3.貨品價格=-1
4.貨品價格=100,付款金額=101
5.貨品價格=100,付款金額=99
6.貨品價格=50,付款金額=100
7.貨品價格=51,付款金額=100
8.貨品價格=90,付款金額=100
9.貨品價格=91,付款金額=100
10.貨品價格=95,付款金額=100
11.貨品價格=96,付款金額=100
12.貨品價格=99,付款金額=100
13.貨品價格=100,付款金額=100
諾伊曼邊界條件
在數學中, 諾伊曼邊界條件(Neumann boundary condition) 也被稱為常微分方程或偏微分方程的“第二類邊界條件”。諾伊曼邊界條件指定了微分方程的解在邊界處的微分。
在常微分方程情況下,如
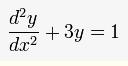 邊界條件
邊界條件在區間[0,1],諾伊曼邊界條件有如下形式:
y'(0) = α1 y'(1) = α2其中α1和α2是給定的數值。
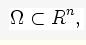 邊界條件
邊界條件一個區域上的偏微分方程,如
Δ y+ y= 0(Δ表示拉普拉斯運算元,諾伊曼邊界條件有如下的形式
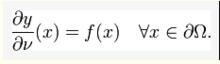 邊界條件
邊界條件這裡,ν表示邊界處(向外的)法向; f是給定的函式。法向定義為
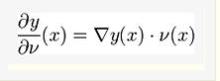 邊界條件
邊界條件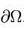 邊界
邊界其中∇是梯度,圓點表示內積。

