排序算法複雜度對比 lgn = log2n基本選擇排序
選擇排序輸出的是原序列的一個重排<a1*,a2*,a3*,...,an*>；，使得a1*<=a2*<=a3*<=...<=an*
排序算法有很多，包括插入排序，冒泡排序，堆排序，歸併排序，選擇排序，計數排序，基數排序，桶排序，快速排序等。插入排序，堆排序，選擇排序，歸併排序和快速排序，冒泡排序都是比較排序，它們通過對數組中的元素進行比較來實現排序，其他排序算法則是利用非比較的其他方法來獲得有關輸入數組的排序信息。
思想
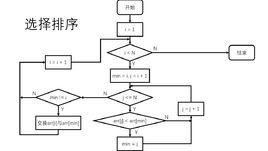
n個記錄的檔案的直接選擇排序可經過n-1趟直接選擇排序得到有序結果：
①初始狀態：無序區為R[1..n]，有序區為空。
②第1趟排序
在無序區R[1..n]中選出關鍵字最小的記錄R[k]，將它與無序區的第1個記錄R[1]交換，使R[1..1]和R[2..n]分別變為記錄個數增加1個的新有序區和記錄個數減少1個的新無序區。
……
③第i趟排序
第i趟排序開始時，當前有序區和無序區分別為R[1..i-1]和R(i..n）。該趟排序從當前無序區中選出關鍵字最小的記錄 R[k]，將它與無序區的第1個記錄R交換，使R[1..i]和R分別變為記錄個數增加1個的新有序區和記錄個數減少1個的新無序區。
解釋
對比數組中前一個元素跟後一個元素的大小，如果後面的元素比前面的元素小則用一個變數k來記住他的位置，接著第二次比較，前面“後一個元素”現變成了“前一個元素”，繼續跟他的“後一個元素”進行比較如果後面的元素比他要小則用變數k記住它在數組中的位置(下標)，等到循環結束的時候，我們應該找到了最小的那個數的下標了，然後進行判斷，如果這個元素的下標不是第一個元素的下標，就讓第一個元素跟他交換一下值，這樣就找到整個數組中最小的數了。然後找到數組中第二小的數，讓他跟數組中第二個元素交換一下值，以此類推。
算法性能
時間複雜度
選擇排序的交換操作介於 0 和 (n - 1） 次之間。選擇排序的比較操作為 n (n - 1） / 2 次之間。選擇排序的賦值操作介於 0 和 3 (n - 1） 次之間。
比較次數O(n^2），比較次數與關鍵字的初始狀態無關，總的比較次數N=(n-1）+(n-2）+...+1=n*(n-1）/2。交換次數O(n），最好情況是，已經有序，交換0次；最壞情況交換n-1次，逆序交換n/2次。交換次數比冒泡排序少多了，由於交換所需CPU時間比比較所需的CPU時間多，n值較小時，選擇排序比冒泡排序快。
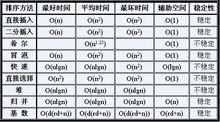
其他排序算法的複雜度如右圖所示。
穩定性
選擇排序是給每個位置選擇當前元素最小的，比如給第一個位置選擇最小的，在剩餘元素裡面給第二個元素選擇第二小的，依次類推，直到第n-1個元素，第n個元素不用選擇了，因為只剩下它一個最大的元素了。那么，在一趟選擇，如果一個元素比當前元素小，而該小的元素又出現在一個和當前元素相等的元素後面，那么交換後穩定性就被破壞了。比較拗口，舉個例子，序列5 8 5 2 9，我們知道第一遍選擇第1個元素5會和2交換，那么原序列中兩個5的相對前後順序就被破壞了，所以選擇排序是一個不穩定的排序算法。
樹形選擇排序
輸入輸出
輸入輸出與基本選擇排序相同。
思想
利用滿二叉樹的性質，將輸入的數據存放到滿二叉樹的葉節點，通過比較樹中剩餘可用節點（從底層的葉節點開始）的大小，每次選擇最小的數值（比較複製到二叉樹的頂端），並且把最小數值賦給排序數組的前端，把最小數值原來葉節點的位置設定為不可用；依次循環直至最後一個可用葉節點。
參考代碼
C語言
C#
C
c++
選擇排序法的第一層循環從起始元素開始選到倒數第二個元素，主要是在每次進入的第二層循環之前，將外層循環的下標賦值給臨時變數，接下來的第二層循環中，如果發現有比這個最小位置處的元素更小的元素，則將那個更小的元素的下標賦給臨時變數，最後，在二層循環退出後，如果臨時變數改變，則說明，有比當前外層循環位置更小的元素，需要將這兩個元素交換.
Java
Golang
Python
Pascal
Perl
php
Ruby
vb
vb實現選擇排序：
排序算法複雜度對比 lgn = log2n