基本思想
選擇排序的基本思想是:每一趟在n-i+1(i=1,2,…n-1)個記錄中選取關鍵字最小的記錄作為有序序列中第i個記錄。基於此思想的算法主要有簡單選擇排序、樹型選擇排序和堆排序。
簡單選擇排序的基本思想:第1趟,在待排序記錄r[1]~r[n]中選出最小的記錄,將它與r[1]交換;第2趟,在待排序記錄r[2]~r[n]中選出最小的記錄,將它與r[2]交換;以此類推,第i趟在待排序記錄r[i]~r[n]中選出最小的記錄,將它與r[i]交換,使有序序列不斷增長直到全部排序完畢。
以下為簡單選擇排序的存儲狀態,其中大括弧內為無序區,大括弧外為有序序列:
初始序列:{49 27 65 97 76 12 38}
第1趟:12與49交換:12{27 65 97 76 49 38}
第2趟:27不動 :12 27{65 97 76 49 38}
第3趟:65與38交換:12 27 38{97 76 49 65}
第4趟:97與49交換:12 27 38 49{76 97 65}
第5趟:76與65交換:12 27 38 49 65{97 76}
第6趟:97與76交換:12 27 38 49 65 76 97 完成
簡單選擇排序的算法具體描述如下:
算法
簡單選擇排序算法分析:在簡單選擇排序過程中,所需移動記錄的次數比較少。最好情況下,即待排序記錄初始狀態就已經是正序排列了,則不需要移動記錄。最壞情況下,需要移動記錄的次數最多為3(n-1)( 此情況中待排序記錄並非完全逆序,給完全逆序記錄排序的移動次數應為(n/2)*3,其中n/2向下取整)。簡單選擇排序過程中需要進行的比較次數與初始狀態下待排序的記錄序列的排列情況無關。當i=1時,需進行n-1次比較;當i=2時,需進行n-2次比較;依次類推,共需要進行的比較次數是∑ =(n-1)+(n-2)+…+2+1=n(n-1)/2,即進行比較操作的時間複雜度為O(n2)。
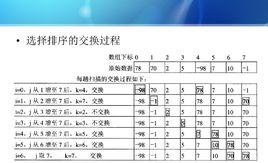
在講選擇排序法之前我們先來了解一下定位比較交換法。為了便於理解,設有10個數分別存在數組元素a[0]~a[9]中。定位比較交換法是由大到小依次定位a[0]~a[9]中恰當的值(和武林大會中的比武差不多),a[9]中放的自然是最小的數。如定位a[0],先假定a[0]中當前值是最大數,a[0]與後面的元素一一比較,如果a[4]更大,則將a[0]、a[4]交換,a[0]已更新再與後面的a[5]~a[9]比較,如果a[8]還要大,則將a[0]、a[8]交換,a[0]又是新數,再與a[9]比較。一輪比完以後,a[0]就是最大的數了,本次比武的武狀元誕生了,接下來從a[1]開始,因為狀元要休息了,再來一輪a[1]就是次大的數,也就是榜眼,然後從a[2]開始,比出探花,真成比武大會了,當比到a[8]以後,排序就完成了。
下面給大家一個例子:
好啦,囉嗦了半天總算把定位比較排序法講完了,這個方法不錯,容易理解,就是有點麻煩,一把椅子換來換去,哎~
所以就有了下面的選擇排序法,開始的時候椅子誰也不給,放在一邊讓大家看著,找個人k記錄比賽結果,然後發椅子。具體來講呢就是,改進定位比較排序法,但是這個改進只是一部分,比較的次數沒變,該怎么打還是怎么打,就是不用換椅子了。每次外循環先將定位元素的小標i值記錄到K,認為a[k]是最大元素其實k=i還是a[ i ]最大,a[k]與後面的元素一一比較,該交換的也交換,就是把K的值改變一下就完了,最後在把a[k]與a[ i ]交換,這樣a就是最大的元素了。然後進入下一輪的比較。選擇排序法與定位比較排序法相比較,比的次數沒變,交換的次數減少了。
下面也寫個例子:
由大到小時:
由小到大時:
有人對上面這兩個算法有一點誤解,原話是這樣說的(“”能看到這裡的都對以上選擇法排序有所疑惑,注意了,以上C語言選擇排序法,都是錯誤的,自己沒有弄清就來誤導別人。而且在網上流傳的選擇排序法大部分都犯的和上面同樣的錯誤。我們來做個邏輯論證,就拿上面這個人說的這個例子,假設第一次比,a[ k ]比a[ j ]比贏了,k變成a[ j ],然後發生第一次交換,第二次比試,a [ k ](這時是a[ j ])又和a[ j +1 ]比,這時沒比贏,不管你怎么比,都要發生第二次交換,因為,第二次的 k 已經變成 j ,再也不等於 i 了。”)這種說法是錯誤的,他很明顯的邏輯錯誤是,假設第一次比贏了,那么進行下一次比較時k的值又再次初始化了,等於此時的i。下面的是一種沒有改進的算法,在內層循環時不管是否改變k的下標,都會進行交換,所以效率會相對低一點。
這個才是真正的選擇排序法,上面那幾個,都是錯誤的。
java選擇排序法代碼