達朗貝爾，J.le R.
正文
又譯達朗伯，法國數學家。1717年11月17日生於巴黎，1783年10月29日卒於巴黎。他是聖讓勒隆教堂附近的一個棄嬰，被一位玻璃匠收養，後來這個教堂的名字就成了他的教名。由於有其生父的暗中資助，他自幼受到良好的教育，早年曾攻讀過神學、法學和醫學，但是後來他發現只有數學才使他確實發生興趣，於是決心獻身數學事業。 達朗貝爾在數學、力學和天文學等許多領域都作出了貢獻。1741年成為法國科學院的院士。1754年被選為法蘭西學院院士，1772年起任學院的終身秘書，是當時法國科學界最有影響的人物之一。1746年，他與著名哲學家D.狄德羅一起編撰法國《百科全書》（1751～1772年出版）並負責撰寫數學與自然科學條目。他還是哲學家，是18世紀法國啟蒙運動的一位傑出代表。
達朗貝爾的《動力學》(1743)是力學方面的一部奠基性著作，書中包括後來以他的名字命名的“達朗貝爾原理”，根據這個原理建立起把動力學問題化為靜力學問題來處理的一般方法。他運用這個方法研究了天體力學中的三體問題，並把它推廣到流體動力學中。
達朗貝爾在弦第一振動理論研究方面的卓越工作，使他和丹尼爾第一·伯努利一起被認為是偏微分方程論的創始人，在他1747年向柏林科學院提交的論文《弦振動研究》中，給出了弦振動方程
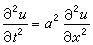
在為微積分奠定理論基礎的漫長過程中，達朗貝爾也作出了重要貢獻。他提出用極限概念代替牛頓的“最初和最終比”。他稱一個量為另一個量的極限，就是後者趨向前者，比任何給定的量都更接近於前者，但不等同於前者。他認為求方程的導數只是要求出方程中所包含的兩個變數的差分之比的極限，他還給出了判別正項級數收斂性的“達朗貝爾法”。
達朗貝爾在1752年關於流體力學的論文中導出了複變函數ƒ(z)=P(x,y)+iQ(x,y)解析的條件：
，
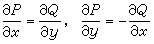達朗貝爾1760 年以後的主要工作包括在他的8卷本的《數學手冊》中。
