根據給定的入射波和測得的散射波研究散射體的特性。它是散射問題的逆問題。由散射波場到散射體特性的反演關係或反演方法,是在散射理論的基礎上獲得的。逆散射理論與反演技術已成為研究各種工程技術和科學問題的一種重要手段。例如,用多頻率或雙極化測量雨反射率、雨衰減或都卜勒譜,可確定雨滴大小分布;在多個頻率或仰角測量大氣輻射噪聲溫度,可推斷大氣層溫度或濕度分布等。逆散射理論與方法廣泛套用於遙感、無損探測、地球物理、醫用成像和雷達目標識別等方面。有兩類逆散射問題,一類是求物體某些物理參數的分布;另一類是根據散射波探求目標物體的幾何形狀。
①求物體某物理參數的分布,如電漿的電子密度剖面。電漿分布在x>0的半無界空間,其電子密度是x坐標的函式,記為N(x)。平面電磁波沿x軸入射到電漿上,產生反射與透射波(一維情況下的散射)。通常的正問題是由電漿上的波方程
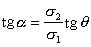 逆散射
逆散射(4)
它給出了由散射波場去重建理想導體目標幾何形狀的有效途徑。
逆散射理論具有廣闊的研究領域。例如,測量中若只得到散射波的強度或微分散射截面,而未得到復振幅中的相位因子,即在測量中丟失了相位信息,通過適當的分析和處理可重新獲得,這一問題稱為相位恢復或相位重建。又如,根據空間某一曲面上的波場分布,尋求波傳播到此曲面以前在另一曲面上的分布,稱為逆衍射問題。此外,還可確定隨機介質或粗糙表面的某種統計特性等。
關於解的存在性、唯一性和穩定性的研究,是反演理論中的重要數學問題。例如,根據散射場的測量數據,特別是有限區域中的測量數據,往往不能唯一地確定散射體。有時,測量數據的某種微小誤差會導致反演結果的極大誤差,因而解是不穩定的。違背上述關於解的三個要求中的一個或數個的問題稱作不適定問題,逆散射問題往往屬於不適定問題。為了去掉不適定性,需要一些附加的限定條件,這種附加條件也稱為先決認識。這種先決認識,可從一般原理、假設、其他實驗結果以及對所做實驗施加的某種限制等推導而知。例如,將散射體區分為理想導體、介質弱散射體或電漿等,便屬於對目標物體的先決認識。