雷達目標和雜波
正文
雷達探測的對象一般稱為雷達目標。凡能散射電磁波的物體都可以作為雷達的目標。空中交通管制雷達以飛機作為目標;艦載雷達以船艦、浮標、海岸線等作為目標;地圖測繪雷達以地面作為目標;氣象雷達以暴風雨等氣象現象作為目標。在雷達目標環境中,目標以外的其他散射體的回波使雷達顯示器上的圖像(或其他形式的雷達輸出信號)變得雜亂,妨礙對目標回波的檢測,稱為雷達雜波。雷達目標和雜波的含義具有相對性,視雷達的用途而定。例如,地面回波對於防空雷達是雜波,而對地形測繪雷達則屬於目標;雲、雨幾乎對所有雷達都是雜波,但對於氣象雷達則屬於目標。散射體分為點散射體和分布散射體。當散射體的尺寸比雷達分辨單元小時,雷達無法分辨其細節,只能把它當作一個點散射體來處理。當散射體的尺寸比雷達分辨單元大時,則須當作分布散射體處理。分布散射體又分為面分布散射體(如地面、海面等)和體分布散射體(如陣雨、鳥群、箔條等)。在多數情況下,雜波是指點目標周圍的分布散射體。廣義地說,雷達雜波還應包括觀測目標以外的無關目標回波和干擾波。
散射體散射能力 雷達必須在雜波、接收機噪聲和其他干擾中檢測目標並提取關於目標的信息。研究目標和雜波的各種性質,對於雷達設計和使用非常必要。目標的散射能力用雷達截面積σ 表示(見雷達目標截面積)。若已知雷達發射功率Pt、天線增益G、天線波束寬度θa(方位)和θe(俯仰)、雷達波長λ、雷達到目標的距離R,則雷達收到的回波功率為
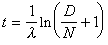 (1)
(1)
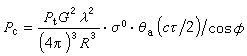 (2)
(2)
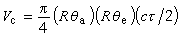 。這時,雷達收到的回波功率
。這時,雷達收到的回波功率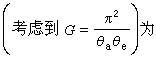
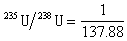 (3)
(3)
回波起伏特性 點目標的尺寸雖比雷達分辨單元小,但可能比雷達波長大得多,形狀可能很複雜,如飛機、船舶等。對於這樣的目標,雷達不能分辨目標各個部分的散射波,只能收到各部分散射波的矢量和。由於目標的運動,雷達照射目標的視角不斷變化。因此,運動目標的回波是起伏的。
回波起伏具有隨機的性質。通常是用機率密度函式P(σ)描述雷達目標截面積起伏幅度分布;用相關函式或傅立葉變換即功率譜密度函式s(f)描述雷達目標截面積起伏的相關特性或頻率分布。面分布和體分布散射體的回波起伏也用同樣方法描述。這些統計性質的實際測量和理論計算是難以做到的。常用理論模型近似地作為實際散射體,以便進行分析和反映回波起伏的基本特點。1960年,P.斯威爾林建立的目標起伏模型有兩種:①把目標看成許多同等大小的獨立散射元的集合,每個散射元的回波幅度相等,相位在0~2π間均勻分布。合成回波的瞬時值服從常態分配,包絡服從瑞利分布,雷達截面積(即回波功率)服從指數分布。具有這種特點的散射體稱為瑞利型(斯威爾林1、2),降雨降雪是典型的瑞利型。例如,從各種角度觀測飛機回波(除側面觀測以外)時,回波起伏均服從瑞利分布。又如,雷達分辨力不高(τ>1微秒,θa>1°)時,低海情(分辨單元大于海浪波長)的海面回波和平坦地面(如沙漠、農田等)的回波,也都服從瑞利分布。②把目標看成一個主要散射元和許多小散射元的集合(斯威爾林3、4)。這時,總的回波功率即散射截面積的機率密度可用4自由度的χ2-分布近似表示(準確的機率密度應為賴斯分布)。當雷達觀測飛機的側面時,其回波起伏符合這種分布。在觀測形狀簡單的大型目標時,測得的大幅度起伏出現的機率比上述模型給出的大,即實際機率密度的尾部比較高。這類目標包括圓柱體和帶翼的圓柱體,如某些衛星體、火箭、艦船和大平板形的目標。在適當選擇參數時,χ2-分布和對數常態分配可以很好地擬合這類目標的實測數據。用高分辨力雷達(τ<1微秒,θa<1°)觀察高海情海面、市區、有建築物的郊區地面時,回波起伏也可用對數常態分配來擬合。這種擬合,僅是用一種便於分析的函式描述實際雜波的起伏特性,而與回波起伏的機理沒有直接的關係。海面雜波和地面雜波往往介於瑞利分布(尾部較低)和對數常態分配(尾部較高)之間。用威布爾分布(形狀參數α在2~0.8之間)能更好的擬合其機率分布。在時間相關性方面,斯威爾林把起伏分為慢起伏和快起伏兩種極端情況。①慢起伏:天線掃描間不相關,掃描內完全相關(斯威爾林1,3);②快起伏:脈衝間不相關(斯威爾林2,4)。實際目標起伏的相關性處於兩者之間。
在分析目標起伏對雷達跟蹤精度的影響和研究抑制雜波的技術時,需要知道目標和雜波起伏功率譜密度函式的具體形式。回波起伏功率譜密度常用高斯函式近似表示為
 。式中fd為目標或雜波的平均都卜勒頻移σf為都卜勒頻移的散布寬度。固定目標(如地物等)的平均都卜勒頻移fd為零,而其散布寬度σf則與天線波束寬度和掃描速度、地面植物搖擺、海浪的運動、飛機姿態角變化快慢等因素有關。運動目標和氣象雜波的fd不為零。氣象雜波的σf與雨滴等散射粒相對運動強度有關。
。式中fd為目標或雜波的平均都卜勒頻移σf為都卜勒頻移的散布寬度。固定目標(如地物等)的平均都卜勒頻移fd為零,而其散布寬度σf則與天線波束寬度和掃描速度、地面植物搖擺、海浪的運動、飛機姿態角變化快慢等因素有關。運動目標和氣象雜波的fd不為零。氣象雜波的σf與雨滴等散射粒相對運動強度有關。 目標識別 當雷達距離分辨力很高時,雷達能觀察到大型目標上各主要散射部位在雷達視線上的分布,並能估計出目標在視線方向上的投影尺寸,加上單脈衝技術還可以測出目標的三維輪廓。利用相干雷達可以測出目標各部分的距離-都卜勒圖像。如果雷達發射波中包含低頻調製分量(波長為目標尺寸的0.5~10倍),如斜坡函式調製,則從雷達回波中可以得到目標尺寸和形狀的信息。這些技術可以用來對目標進行分類和識別。金屬目標上各部分之間的接觸達不到分子水平而間隙又小到 100埃數量級時,其接觸面呈現出非線性效應。這時,散射波中包含入射波的高次諧波和多種頻率入射波的交叉波。諧波的強度不再與入射波強度成正比,而是成非線性函式,即在諧波上雷達截面積與入射功率有關。利用這種效應,在高次諧波上(常用三次諧波)接收目標回波,可以區分金屬與非金屬目標,並可用來抑制雜波。
 雷達目標和雜波
雷達目標和雜波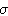 0與雷達頻段、極化和入射餘角的關係。圖中數據是多次測量的平均值。接近垂直照射時,海面的鏡面反射很強。入射餘角很小時,入射波與反射波(兩者反相)發生干涉,使後向散射變弱。測量表明,當風速低於5節時,海面後向散射很小。當風速從5節增大到20節時,後向散射增加很快,到20節時接近飽和。雷達截面積密度σ0與風速的關係是σ0正比於e
0與雷達頻段、極化和入射餘角的關係。圖中數據是多次測量的平均值。接近垂直照射時,海面的鏡面反射很強。入射餘角很小時,入射波與反射波(兩者反相)發生干涉,使後向散射變弱。測量表明,當風速低於5節時,海面後向散射很小。當風速從5節增大到20節時,後向散射增加很快,到20節時接近飽和。雷達截面積密度σ0與風速的關係是σ0正比於e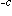 /V。式中V為風速;c為常數。
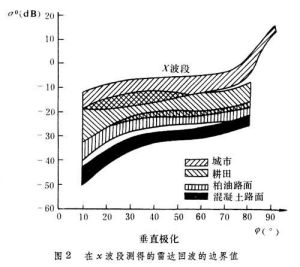
/V。式中V為風速;c為常數。 對於地面回波,不論在理論上還是在實際上都比海面回波存在更多的問題。一般來說,地面回波比海面回波強。只是在垂直照射時地面回波較弱。地面回波隨地形和地貌變化很大。山地、平原、沙漠、耕地、沼澤、不同的植被(樹木、莊稼)、植物的不同生長期、地面上的建築物等,都有不同的散射特性。圖2表示不同地面的散射截面積密度σ0的典型數值範圍。
 雷達目標和雜波
雷達目標和雜波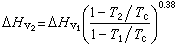
 ;ε為雨滴的介電常數;Di為雨滴直徑。
;ε為雨滴的介電常數;Di為雨滴直徑。 單只的鳥和昆蟲的雷達截面積很小,成群的鳥和昆蟲也能嚴重地干擾對目標的觀測。利用靈敏度時間控制電路可以抑制近距離的鳥群回波。
至於由大氣折射係數不均勻和“睛空湍流”造成的後向散射(即“仙波”),只有在雷達發射功率很大時才能觀察得到。
