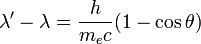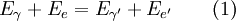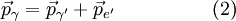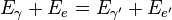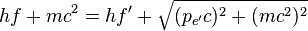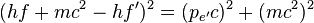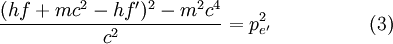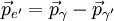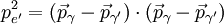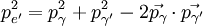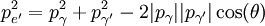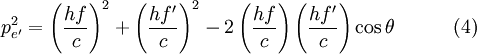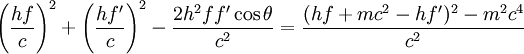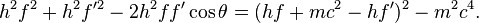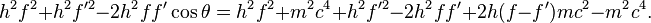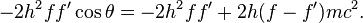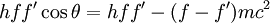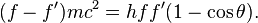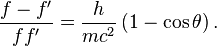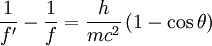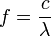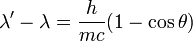康普頓散射

康普頓散射

康普頓散射或康普頓效應，是指當X射線或伽馬射線的光子跟物質相互作用，因失去能量而導致波長變長的現象。

物理學中，康普頓散射或康普頓效應，是指當X射線或伽馬射線的光子跟物質相互作用，因失去能量而導致波長變長的現象。相應的還存在逆康普頓效應——光子獲得能量引起波長變短。

這一波長變化的幅度被稱為康普頓偏移。

康普頓效應通常只指物質電子云與光子的相互作用，但還有物質原子核與光子的相互作用——核康普頓效應存在。

簡介

康普頓效應在1923年被阿瑟·霍利·康普頓觀察到，並在隨後的幾年間由他的研究生吳有訓進一步證實。阿瑟·康普頓因發現此效應而獲得1927年諾貝爾物理學獎。

這個效應反映出光不僅僅具有波動性。此前湯姆生散射的經典波動理論並不能解釋此處波長偏移的成因，必須引入光的粒子性。這一實驗說服了當時很多物理學家相信，光在某種情況下表現出粒子性，光束類似一串粒子流，而該粒子流的能量與光頻率成正比。

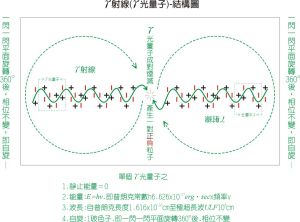
電子-內部結構模型圖電子-內部結構模型圖

在引入光子概念之後，康普頓散射可以得到如下解釋：電子與光子發生彈性碰撞，電子獲得光子的一部分能量而反彈，失去部分能量的光子則從另一方向飛出，整個過程中總動量守恆，如果光子的剩餘能量足夠多的話，還會發生第二次甚至第三次彈性碰撞。

康普頓散射可以在任何物質中發生。光子能量範圍在0.5至3.5電子伏特時比較容易觀測到，能量過高的光子﹝例如是可見光或更高頻率的光子﹞，則可能彈出電子而發生光電效應。

康普頓頻移公式

康普頓本人引用光電效應和狹義相對論來解釋這一現象，並依據餘弦定律推導得出康普頓頻移公式

康普頓散射\lambda' - \lambda = \frac{h}{m_e c}(1-\cos{\theta})

其中

λ為散射之前的波長
λ' 為散射之後的波長
me為電子質量
θ為光子方向轉動角﹝散射前與散射後的路徑夾角﹞，
h為普朗克常數以及
c為光速。
h/(mec)=2.43×10-12 米，被稱為康普頓波長。

推導過程

根據能量及動量守恆定律，有：

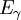康普頓散射E_\gamma + E_e = E_{\gamma^\prime} + E_{e^\prime} \quad \quad (1) \,
康普頓散射\vec p_\gamma = \vec{p}_{\gamma^\prime} + \vec{p}_{e^\prime} \quad \quad \quad \quad \quad (2) \,

其中

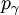康普頓散射E_\gamma \,和康普頓散射p_\gamma \,是光子的能量和質量，而
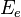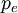康普頓散射E_e \,和康普頓散射p_e \,則是電子的能量和質量。

解方程(1)

現在計算能量的差值:

康普頓散射E_{\gamma} + E_{e} = E_{\gamma'} + E_{e'}\,
康普頓散射hf + mc^2 = hf' + \sqrt{(p_{e'}c)^2 + (mc^2)^2}\,

解此方程得pe':

康普頓散射(hf + mc^2-hf')^2 = (p_{e'}c)^2 + (mc^2)^2\,
康普頓散射\frac{(hf + mc^2-hf')^2-m^2c^4}{c^2}= p_{e'}^2 \quad \quad \quad \quad \quad (3) \,

解方程(2)

從方程(2)得

康普頓散射\vec{p}_{e'} = \vec{p}_\gamma - \vec{p}_{\gamma'} \,

平方後可得

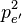康普頓散射p_{e'}^2 = (\vec{p}_\gamma - \vec{p}_{\gamma'}) \cdot (\vec{p}_\gamma - \vec{p}_{\gamma'})
康普頓散射p_{e'}^2 = p_{\gamma}^2 + p_{\gamma'}^2 - 2\vec{p_{\gamma}} \cdot \vec{p_{\gamma'}}
康普頓散射p_{e'}^2 = p_\gamma^2 + p_{\gamma'}^2 - 2|p_{\gamma}||p_{\gamma'}|\cos(\theta) \,
康普頓散射p_{e'}^2 = \left(\frac{h f}{c}\right)^2 + \left(\frac{h f'}{c}\right)^2 - 2\left( \frac{hf}{c} \right) \left(\frac{h f'}{c} \right) \cos{\theta} \quad \quad \quad (4)

整理

現有表示康普頓散射p_{e'}^2 (eq 3 & 4)的兩條方程，將兩式同等後得：

康普頓散射\left(\frac{h f}{c}\right)^2 + \left(\frac{h f'}{c}\right)^2 - \frac{2h^2 ff'\cos{\theta}}{c^2} = \frac{(hf + mc^2-hf')^2 -m^2c^4}{c^2} \,

現在開始簡化。首先兩邊一同乘上c2 ：

康普頓散射h^2 f^2 + h^2 f'^2 - 2h^2 ff' \cos \theta = (hf + mc^2 - hf')^2 - m^2c^4 . \,

然後，將右方展開：

康普頓散射h^2f^2+h^2f'^2-2h^2ff'\cos{\theta} = h^2f^2+m^2c^4+h^2f'^2-2h^2ff'+2h(f-f')mc^2 -m^2c^4 .\,

兩邊有幾個項互相抵消，得

康普頓散射-2h^2ff'\cos{\theta} = -2h^2ff'+2h(f-f')mc^2 .\,

然後兩邊同除以" − 2h"得

康普頓散射hff'\cos{\theta} = hff'-(f-f')mc^2 \,
康普頓散射(f-f')mc^2 = hff'(1-\cos{\theta}) .\,

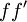兩邊同除以mc2 然後再除以康普頓散射ff^\prime:

康普頓散射\frac{f-f^\prime}{f f^\prime} = \frac{h}{mc^2}\left(1-\cos \theta \right) . \,

現在左方可以重寫並簡化成

康普頓散射\frac{1}{f^\prime} - \frac{1}{f} = \frac{h}{mc^2}\left(1-\cos \theta \right) \,

這方程跟康普頓散射公式是一致的，但一般多用λ表示而少用f。使用下式作轉換

康普頓散射f=\frac{c}{\lambda} \,

所以最後得,

康普頓散射\lambda'-\lambda = \frac{h}{mc}(1-\cos{\theta}) \,

套用

康普頓散射

康普頓效應對放射生物學十分重要，由於它是高能量X射線與生物中的原子核間，最有可能發生的相互作用，因此亦被套用於放射療法。

材料物理中，康普頓效應可以用於探測物質中的電子波函式。

康普頓效應也是伽馬射線光譜學中的重要效應，它是導致﹝光譜圖表上﹞康普頓邊緣的原因，因為伽馬射線有可能被散射出所用的探測器以外。康普頓抑壓法﹝用較廉價的探測器去包圍較高價的主探測器﹞被用於探測走散的散射伽馬射線而抵消此作用帶來的影響。

逆康普頓散射

逆康普頓散射在天體物理學上有重要意義。在X射線天文學中，黑洞周圍的吸積盤被認為會產生熱輻射。此輻射所產生的低能光子會與黑洞的暈中的相對論性電子發生逆康普頓散射，從而獲得能量。此現象被視為是吸積黑洞的X射線光譜﹝0.2-10千電子伏﹞中冪次項的成因。

當宇宙微波背景輻射穿過星系團周圍的熱氣體時，逆康普頓效應亦能被觀測到。宇宙微波背景輻射的光子被氣體中的電子散射到更高的能量去，即所觀測到的蘇尼亞耶夫-澤爾多維奇效應

相關詞條

相關搜尋

熱門詞條

聯絡我們