定義
入射到近軸球面上並與光軸(z 軸)的夾角很小的光線稱為近軸光線。
 近軸光線
近軸光線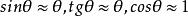 近軸光線
近軸光線設近軸光線與光軸的夾角為 ,則 。(因為是近軸光線,α角很小,趨近於0。另外,通過光學系統之後,近軸光線可認為交於一點)
近軸光線是一種物理模型。是指可以用斯涅耳折射定理(光的折射定律)來描述的光線。這一類光線離主光軸的距離可以認為是0。它可以把問題簡化,因此是一種常用的模型。
符號規則
設在空間存在如下一個折射球面:
 近軸光線
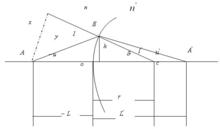
近軸光線r:折射球面曲率半徑;o:頂點;L:物方截距;L':像方截距;u:物方孔徑角;u':像方孔徑角;
符號規則:光線方向自左向右
(1) 沿軸線段:以頂點O為原點,光線到光軸交點或球心,順光線為正,逆光線為負。
(2) 垂軸線端:光軸以上為正,光軸以下為負。
(3) 光線與光軸夾角:由光軸轉向光線銳角,順時針為正,逆時針為負。
(4) 光線與折射面法線的夾角:由光線經銳角轉向法線,順時針為正,逆時針為負。
(5) 光軸與光線的夾角:有光軸經銳角轉向法線,順時針為正逆時針為負。
(6) 折射面間隔:d有前一面頂點到後一面頂點方向,順光線方向為正,逆光線方向為負。
光路計算
公式:
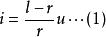 近軸光線
近軸光線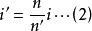 近軸光線
近軸光線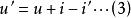 近軸光線
近軸光線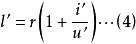 近軸光線
近軸光線由(1)、(2)、(3)、(4)推出
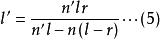 近軸光線
近軸光線(5)式說明:在近軸區l’只是l的函式,它不隨孔徑u的變化而變化,軸上物點在近軸區成完善像,這個像點稱高斯像點。
高斯像面:通過高斯像點且垂直於光軸的平面稱為高斯像面。
共軛點:像上面提到的一對構成物象關係的點稱為共軛點。
在近軸區有:
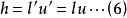 近軸光線
近軸光線由公式(1)(2)(3)(4)(5)(6)可推出:
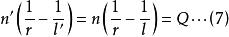 近軸光線
近軸光線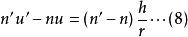 近軸光線
近軸光線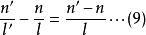 近軸光線
近軸光線(7)式中Q稱為阿貝不變數,對於單個折射球面物空間與像空間的Q相等;
(8)式表明了物、像孔徑角的關係
(9)式表明了物、像位置關係
限制了光線與光軸的夾角,光線在折射面上 的入射角,折射角等都很小.所有角度小於5°正切,正弦都可用該角度的弧度值代替。
近軸範圍
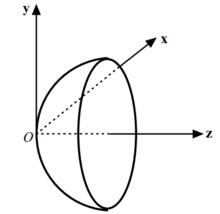 透鏡曲面方程所採用的坐標系
透鏡曲面方程所採用的坐標系在光學系統的近軸範圍內,其折射面或反射面的面形可以由下式表示:
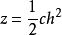 近軸光線
近軸光線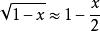 近軸光線
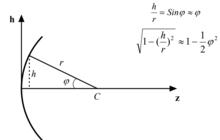
近軸光線現以球面為例看看這個近軸球面定義的實質,由球面方程考查比較。如果h與r相比很小,允許取近似。則有
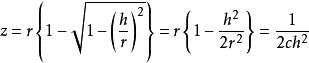 近軸光線
近軸光線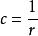 近軸光線
近軸光線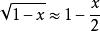 近軸光線
近軸光線其中,,即在近軸範圍里,允許作這種近似。它是一個近軸球面,h遠小於近軸球面半徑r。
 近軸範圍
近軸範圍列矩陣表示
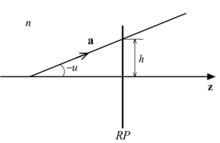 近軸光線的表示
近軸光線的表示含光軸面(紙面)內的任一近軸光線可用該光線在參考面上的投射高度h,以及它與光軸的夾角μ(即孔徑角)這兩個參數來表示。又為了表明該光線所在的媒質折射率n,將n與μ的乘積nμ作為一個參數,稱謂光學方向餘弦。這樣,光線可用列矩陣a表示,即
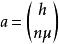 近軸光線
近軸光線近軸光線的折射矩陣
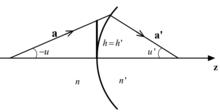 近軸球面對近軸光線的折射
近軸球面對近軸光線的折射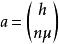 近軸光線
近軸光線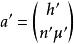 近軸光線
近軸光線如圖所示是一個近軸折射球面,兩邊媒質的折射率分別為n和n’,近軸球面半徑為r。近軸光線,入射到這個近軸球面上,經其折射成為折射光線。
將參考面取在過近軸球面頂點的切平面上,由近軸光線的性質知,如下關係成立h'=h。
近軸光線在近軸球面上折射前後滿足關係:
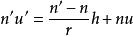 近軸光線
近軸光線兩式聯立並寫成矩陣形式有:
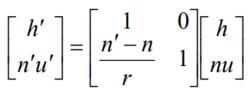 近軸光線
近軸光線方陣只含有近軸球面系統的參量。稱其為近軸光線的折射矩陣,用R簡記之 ,即
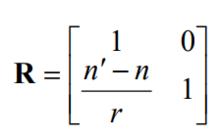 近軸光線
近軸光線套用
近軸光線一般被套用於高斯光學。幾何光學中研究和討論光學系統理想成像性質的分支稱為高斯光學(或近軸光學)。它通常只討論對某一軸線(即光軸)具有旋轉對稱性的光學系統。
