定義
在一個含有若干個元的多項式中,如果任意交換兩個元的位置,多項式不變,這樣的多項式叫做對稱多項式。
輪換式與對稱式
如果一個多項式中的變數字母按照任何次序輪換後,原多項式不變,那么稱該多項式是輪換多項式。 對稱輪換式就是兩項互換,可以看做輪換式的特殊情況。
下面通過例子來說明輪換式和對稱式的區別和聯繫:
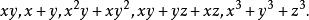 輪換式
輪換式1、對於這幾個代數式:
交換這些式子中的任意兩個字母,式子不變。我們把這樣的式子叫做 對稱式。
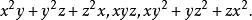 輪換式
輪換式2、再看這幾個式子:
將這些式子中的 x 換成 y, 將 y 換成 z, 將 z 換成 x,即將字母做一個輪換, 式子保持不變。我們將這樣的式子叫做 輪換式。
由此可見: 對稱式一定是輪換式,但輪換式未必是對稱式。另外,兩個輪換式(對稱式)的和、差、積、商仍然是輪換式(對稱式)。
輪換式的因式分解
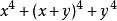 輪換式
輪換式例1:分解因式
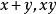 輪換式
輪換式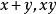 輪換式
輪換式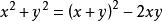 輪換式
輪換式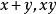 輪換式
輪換式分析: 這是一個二元對稱式,二元對稱式的基本對稱式是 .任何二元對稱多項式都可用 表示,如 ,二元對稱多項式的分解方法之一是:先將原式用 表示,再行分解。
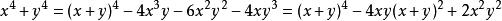 輪換式
輪換式解:
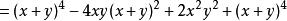 輪換式
輪換式∴原式
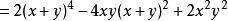 輪換式
輪換式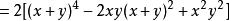 輪換式
輪換式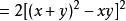 輪換式
輪換式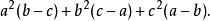 輪換式
輪換式例2:分解因式
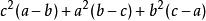 輪換式
輪換式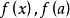 輪換式
輪換式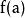 輪換式
輪換式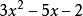 輪換式
輪換式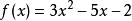 輪換式
輪換式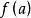 輪換式
輪換式 輪換式
輪換式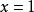 輪換式
輪換式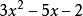 輪換式
輪換式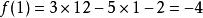 輪換式
輪換式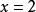 輪換式
輪換式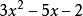 輪換式
輪換式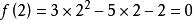 輪換式
輪換式此題中若將式中的b換成a,c換成b,a換成c,即為 ,原式不變,這類多項式稱為關於a、b、c的輪換對稱式,輪換對稱式的因式分解,用因式定理及待定係數法比較簡單。下面先粗略介紹一下因式定理,為了敘述方便先引入符號 , 如對一元多項式 可記作 , 即表示當 時多項式的值,如 時,多項式 的值為 ;當 時多項式 的值為
 輪換式
輪換式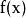 輪換式
輪換式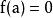 輪換式
輪換式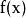 輪換式
輪換式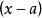 輪換式
輪換式 輪換式
輪換式因式定理:如果 時多項式 的值為零,即 則 能被 整除(即含有 的因式)。
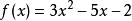 輪換式
輪換式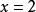 輪換式
輪換式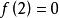 輪換式
輪換式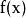 輪換式
輪換式 輪換式
輪換式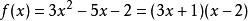 輪換式
輪換式如多項式 ,當 時, 即 含有 的因式,事實上 .
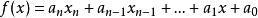 輪換式
輪換式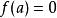 輪換式
輪換式對於一般的形式: ,若 ,則
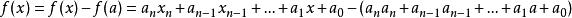 輪換式
輪換式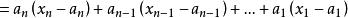 輪換式
輪換式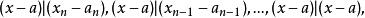 輪換式
輪換式由於 (其中 | 表示整除)
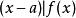 輪換式
輪換式∴
由以上分析可知:對於多元多項式,在使用因式定理時可以確定一個主元,而將其它的元看成確定的數來處理.
我們利用因式定理來解例2:
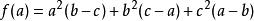 輪換式
輪換式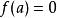 輪換式
輪換式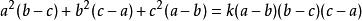 輪換式
輪換式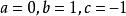 輪換式
輪換式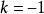 輪換式
輪換式解 這是一個含有a、b、c三個字母的三次多項式,現以a為主元,設 ,易知當a=b和a=c時,都有 ,故a-b和a-c是多項式的因式,而視b為主元時,同理可知b-c也是多項式的因式,而三次多項式至多有三個因式故可設 ,其中k為待定係數,令 可得
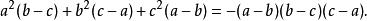 輪換式
輪換式∴
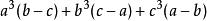 輪換式
輪換式例3分解因式
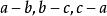 輪換式
輪換式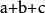 輪換式
輪換式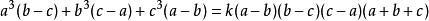 輪換式
輪換式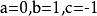 輪換式
輪換式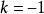 輪換式
輪換式分析: 這是一個關於a、b、c的四次齊次輪換多項式,可用因式定理分解,易知 是多項式的三個因式,而四次多項式還有一個因式,由輪換對稱性可知這個一次因式應是 ,故可設 (其中k為待定係數),取 可得 ,所以
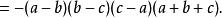 輪換式
輪換式原式
輪換式的形式
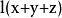 輪換式
輪換式一次齊次的輪換式形如:
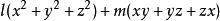 輪換式
輪換式二次齊次的輪換式形如:
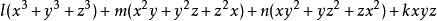 輪換式
輪換式三次齊次的輪換式形如:
其中的 l, m, n, k 是待定常數.
齊次與非齊次
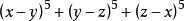 輪換式
輪換式分解因式
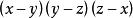 輪換式
輪換式易知其有因式 。因為原式是五次齊次輪換式,所以還缺一個二次齊次輪換式。不妨設
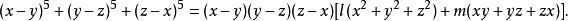 輪換式
輪換式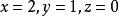 輪換式
輪換式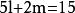 輪換式
輪換式令 可得
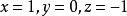 輪換式
輪換式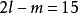 輪換式
輪換式令 可得
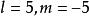 輪換式
輪換式於是可得 。這就給出了所要的因式分解。
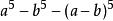 輪換式
輪換式分解因式:
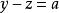 輪換式
輪換式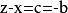 輪換式
輪換式記 , 則此題就變為上一例題。最後結果為:
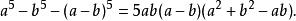 輪換式
輪換式一個有用的公式
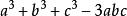 輪換式
輪換式分解因式:
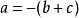 輪換式
輪換式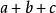 輪換式
輪換式當 時,原式為 0,所以原式有因式 。再者,原式是三次齊次輪換式,所以我們還缺一個二次齊次輪換式因式。 不妨設
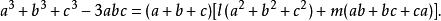 輪換式
輪換式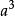 輪換式
輪換式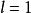 輪換式
輪換式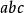 輪換式
輪換式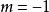 輪換式
輪換式比較兩邊 的係數可得 。比較 的係數可得 ,於是:
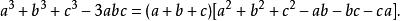 輪換式
輪換式有時候我們也把它寫為
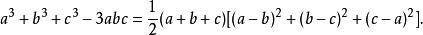 輪換式
輪換式