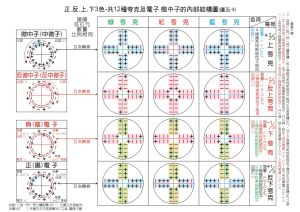
費米子-內部結構模型圖根據量子力學，費米子為自旋為半整數的粒子，其本徵波函式反對稱，在費米子的某一個能級上，最多只能容納一個粒子。因而符合費米-狄拉克統計分布的粒子，當他們處於某一分布<math>\left\{ n_j \right\}</math>（“某一分布”指這樣一種狀態：即在能量為<math>\left\{ \epsilon_j \right\}</math>的能級上同時有<math>n_j</math>個粒子存在著，不難想像，當從巨觀觀察體系能量一定的時候，從微觀角度觀察體系可能有很多種不同的分布狀態，而且在這些不同的分布狀態中，總有一些狀態出現的幾率特別的大，而其中出現幾率最大的分布狀態被稱為最可幾分布）時，體系總狀態數為：
<math>
\Omega_j=\frac{g_j!}{n_j!(g_j-n_j)!} </math>
費米-狄拉克統計的最可幾分布的數學表達式為：
<math>
\left\{ n_j^{FD} \right\}=\frac{g_j e^\alpha e^{\beta\epsilon_j}}{1 + e^\alpha e^{\beta\epsilon_j}} </math>
由於費米-狄拉克統計在數學處理上非常困難，因此在處理實際問題時經常引入一些近似條件，使費米-狄拉克統計和玻色-愛因斯坦統計退化成為經典的麥克斯韋-玻爾茲曼統計。
