定義
費米子是 自鏇為半整數( 即自鏇為/2，=h/2π，h是普朗克常量）的粒子，如輕子和重子，全同費米子系統中粒子不可分辨，費米子遵從泡利不相容原理，每一量子態容納的粒子數不能超過一個。對於粒子數、體積和總能量確定的費米子系統，當溫度為T時 ，處在能量為的量子態上的平均粒子數為
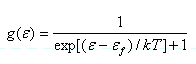費米-狄拉克分布公式式中，k是玻耳茲曼常量，εf是化學勢。在高溫和低密度條件下，費米-狄拉克分布過渡到經典的麥克斯韋-玻爾茲曼分布。
歷史
1926年發現費米–狄拉克統計之前，要理解電子的某些性質尚較為困難。例如，在常溫下，未施加電流的金屬內部的熱容比施加電流的金屬少了大約100倍。此外，在常溫下給金屬施加一強電場，將造成場致電子發射（Field electron emission）現象，從而產生電流流經金屬。研究發現，這個電流與溫度幾乎無關。當時的理論難以解釋這個現象。
當時，由於人們主要根據的是經典靜電學理論，因此在諸如金屬電子理論等方面遇到的困難，無法得到令人滿意的解答。他們認為，金屬中所有電子都是等效的。也就是說，金屬中的每個電子都以相同的程度對金屬的熱量做出貢獻（這個量是波爾茲曼常數的一次項）。上述問題一直困擾著科學家，直到費米–狄拉克統計的發現，才得到較好地解釋。
1926年，恩里科·費米、保羅·狄拉克各自獨立地在發表了有關這一統計規律的兩篇學術論文。。另有來源顯示，P·喬丹（Pascual Jordan）在1925年也對這項統計規律進行了研究，他稱之為“泡利統計”，不過他並未及時地發表他的研究成果。狄拉克稱此項研究是費米完成的，他稱之為“費米統計”，並將對應的粒子稱為“費米子”。
1926年，拉爾夫·福勒在描述恆星向白矮星的轉變過程中，首次套用了費米–狄拉克統計的原理。1927年，阿諾·索末菲將費米–狄拉克統計套用到他對於金屬電子的研究中。。1928年，福勒和L·W·諾德漢（Lothar Wolfgang Nordheim）在場致電子發射的研究中，也採用了這一統計規律。直至今日，費米–狄拉克統計仍然是物理學的一個重要部分。
