概念
解向量是線性方程組的一個解。因為一組解在空間幾何里可以表示為一個向量,所以叫做解向量。解向量在矩陣和線性方程組中是常用概念。
 解向量
解向量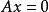 解向量
解向量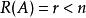 解向量
解向量 解向量
解向量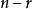 解向量
解向量如果元齊次線性方程組係數矩陣的秩,則解空間的基礎解系存在,且每個基礎解系恰有個解向量。
基本原理
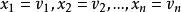 解向量
解向量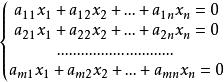 解向量
解向量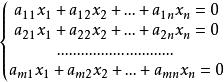 解向量
解向量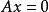 解向量
解向量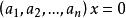 解向量
解向量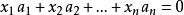 解向量
解向量設是齊次線性方程組的解,則稱向量為方程組的解向量,它同時也是、和這些式子的解。
齊次線性方程組的解向量有如下的性質:
性質1:若
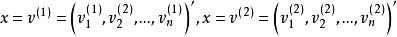 解向量
解向量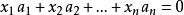 解向量
解向量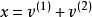 解向量
解向量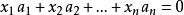 解向量
解向量是式子的解,則也是式子的解。
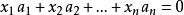 解向量
解向量證明:根據式子證明。由假設,有
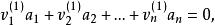 解向量
解向量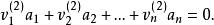 解向量
解向量將上面二等式的兩端分別相加,得:
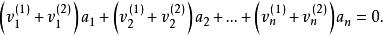 解向量
解向量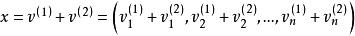 解向量
解向量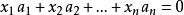 解向量
解向量這就證明了是的解。
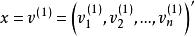 解向量
解向量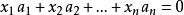 解向量
解向量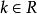 解向量
解向量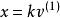 解向量
解向量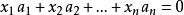 解向量
解向量性質2:若是式子的解,,則也是式子的解。
證明:由假設,有:
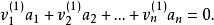 解向量
解向量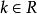 解向量
解向量顯然,對於任意的,有:
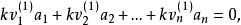 解向量
解向量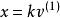 解向量
解向量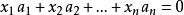 解向量
解向量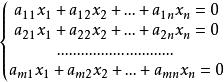 解向量
解向量即是式子也即的解。

