基本介紹
西爾維斯特問題是涉及構造直線的組合幾何的難題，英國數學家西爾維斯特(J.J.Sylvester)晚年研究過這樣一個問題：在平面內找出不共線的n個點構成的點集S，使其中任意兩點的連線必過S中的不同於這兩點的第三點。經過反覆研究，他覺察到這是不可能的，但他不能給予證明，於是，他在1893年的《教育時代》雜誌中提出下面的猜想徵求解答：設S是平面有限點集，且過其中任意兩點的直線必過S中的其他一點，證明S的點共線。
西爾維斯特問題的解答
西爾維斯特問題提出後很長時間未獲得解決，40年後，1933年，伽萊(T.Gallai)發表了一個相當複雜的證明，證明了西爾維斯特猜想是正確的，1943年，匈牙利數學家愛爾特希(P.Erdös)在《美國數學月刊》上重提西爾維斯特問題，第二年，多倫多大學的羅伯特·斯坦伯格給出了一個簡單的初等證明，1948年，凱利(L.M.Kelly)發表了一個更精巧的證明，比斯坦伯格的還要簡捷，以至於美國的《科學新聞》在1979年重提西爾維斯特問題時，稱之為“可簡捷解答的難題”，這兩個人的證明還有一個重要的差別：斯坦伯格的證明雖然長了一些，但不必使用距離概念，只涉及順序，因而在理論上更有意義。
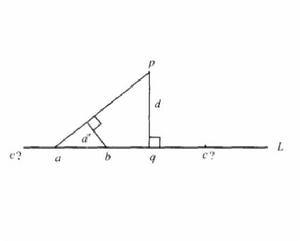
凱利的證明 假設這些具有西爾維斯特所述性質的點不共線，每條經過其中兩點的直線L和不在這條直線上的一個點p都組成一個線點對(L，p)，在所有這些線點對中選取一個使得從p到L的距離d為最小的。令q為從p向L所引垂線的垂足。於是(變分)根據假設，在L上至少存在三個點a，b和c。因此其中兩個點，比方說a和b，將以a，b，q的順序位於q的同一側(c可在任何一側)，如圖1，但這樣從b到直線ap的距離d'就小於d，這就產生了一個矛盾。
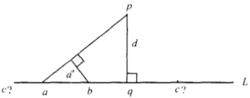圖1凱利的證明確實簡短——但是，這裡有考克斯特(H.S.M.Coxeter)的說法：“這件關於共線性的事[西爾維斯特的問題]顯然屬於序幾何。[確實，在複數域或有限域上這個結果不成立!你可以輕易地在環面上發現一個九點的反例。]凱利的歐氏幾何式證明涉及外在的距離概念：這好比用一把長柄錘子去砸一個杏仁。”
西爾維斯特猜想的證實，等價於下面命題的正確性：設S是平面有限點集，且這些點不共線，則必有隻經過其中兩點的直線，這直線一般稱為點集S的平凡直線，由n個不共線的點構成的點集S中，所有的平凡直線的條數記為S(n)，圍繞著S(n)尚未解決的問題有：
1.S(n)的最小值問題，即不共線n點集最少有多少條平凡直線?已知的結果是
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ||
| S(n)最小值 | 3 | 3 | 4 | 3 | 3 | 4 | 6 | 5 | 6 | 6 | 6 | 7 | ||
n≥15的S(n)尚不知曉。
2.莫茨金-迪拉克猜想。1951年，莫茨金(T.Motzkin)和迪拉克(H.Dulac)各自獨立地做出下列猜想：對任何不共線的n點集，都有
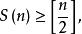西爾維斯特問題式中[n/2]表示不大於n/2的最大整數。
1958年，凱利與莫澤(W.O.Moser)合作證明了
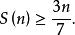西爾維斯特問題1981年，漢森(S.Hansen)證明了，除n=7，13外，都有
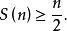西爾維斯特問題這是一個長達96頁的證明，用了27個引理、41個輔助圖。
