簡介
複測度是取復值的可列可加集函式。
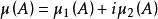 複測度
複測度設μ與μ為可測空間(Ω,)上的廣義(實值)測度,則對任意A∈,由 確定的上的集函式μ稱為(Ω,)上的複測度。
性質
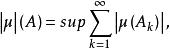 複測度
複測度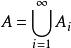 複測度
複測度若μ為(Ω,)上的複測度,對任意A∈,定義 這裡的上確界是對A的所有分劃{A}(亦即 ,每個A∈,i≠j時A∩A=∅)取的,可證集函式|μ|是一個測度,且存在可測函式h,使得|h(x)|=1對所有x∈Ω成立,還有dμ=hd|μ|。此式稱為複測度μ的極分解。
可列可加集函式
可列可加集函式亦稱完全可加集函式或可數可加集函式,是一類特殊而又重要的集函式。
設μ是定義在集類上的集函式,若對任意A,B∈,A∪B∈,A∩B=∅,都有μ(A∪B)=μ(A)+μ(B),則說μ具有有限可加性。
