complex method
求解最最佳化問題的一種算法。該法較為適合解決有約束最佳化問題。使用該法僅需比較目標函式值即可決定搜尋方向，算法較簡單，對目標函式的要求不苛刻。
複合形法
複合形法複合形是多個單純形合併成的超多面體，頂點個數（維空間）。
複合形法與單純形法極為相似，卻也有不同：
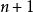複合形法
複合形法1）複合形法不限制頂點個數為，複合形法的頂點個數k取值範圍為；
2）複合形法需要檢查頂點的可行性，即是否滿足約束。
複合形法是由n+1個以上的頂點組合而成的多面體。他的基本思路是：在可行域內構造一初始複合型，然後通過比較各頂點目標函式值，在可行域中找一目標函式值有所改善的新點，並用其替換目標函式值較差的頂點，構成新的複合形。不斷重複上述過程，複合形不斷變形、轉移、縮小，逐漸地逼近最優點。當複合形各頂點目標函式值相差不大或者各頂點相距很近時，則目標函式值最小的頂點即可作為最優點。複合形點點數目k一般取值(n+1)≤k≤2n，n是設計變數的個數。為了減小計算變數，複合形法在尋優過程中一般只以在可行域內的反射作為基本搜尋策略。
複合形法尋優方法主要工作是生成初始複合形和更新複合形。
綜合來說複合型法的算法思路清晰，容易掌握；不需求導數，不需作一維搜尋，對函式性態沒有特殊要求；程式結構簡單，計算量不大；對初始點要求低，能較快地找到最優解，算法較為可靠。求解時需給出變數取值區間及初始複合形；隨著變數維數增多計算效率明顯降低；對約束條件較多的非凸問題，常出現多次想形心收縮，使收斂速度減慢。
複合形法適用於變數少，最好不超過15維，約束條件不多的最佳化問題。是機械最佳化設計中較為廣泛的可靠算法之一。
