簡介
薛丁格繪景(Schrödinger picture)是量子力學的一種表述,為紀念物理學者埃爾溫·薛丁格而命名。在薛丁格繪景里,量子系統的態矢量隨著時間流易而演化,而像位置、自旋一類的對應於可觀察量的算符則與時間無關。
薛丁格繪景與海森堡繪景、狄拉克繪景不同。在海森堡繪景里,對應於可觀察量的算符會隨著時間流易而演化,而描述量子系統的態矢量則與時間無關。在狄拉克繪景里,態矢量與算符都會隨著時間流易而演化。
這三種繪景殊途同歸,所獲得的結果完全一致。這是必然的,因為它們都是在表達同樣的物理現象。
 薛丁格繪景
薛丁格繪景 薛丁格繪景
薛丁格繪景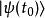 薛丁格繪景
薛丁格繪景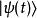 薛丁格繪景
薛丁格繪景在薛丁格繪景里,負責時間演化的算符是一種么正算符,稱為時間演化算符。假設時間從 流易到 ,而經過這段時間間隔,態矢量 演化為態矢量 ,這時間演化過程以方程表示為
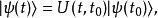 薛丁格繪景
薛丁格繪景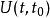 薛丁格繪景
薛丁格繪景其中, 是時間演化算符。
假設系統的哈密頓量H不含時,則時間演化算符為
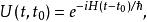 薛丁格繪景
薛丁格繪景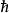 薛丁格繪景
薛丁格繪景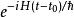 薛丁格繪景
薛丁格繪景其中, 是約化普朗克常數,指數函式 必須通過其泰勒級數計算。
在初級量子力學教科書里,時常會使用薛丁格繪景。
時間演化算符
定義
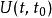 薛丁格繪景
薛丁格繪景時間演化算符 定義為
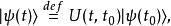 薛丁格繪景
薛丁格繪景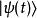 薛丁格繪景
薛丁格繪景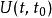 薛丁格繪景
薛丁格繪景 薛丁格繪景
薛丁格繪景其中,右矢 表示時間為t的態矢量, 是時間演化算符,從時間t演化到時間 。
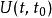 薛丁格繪景
薛丁格繪景 薛丁格繪景
薛丁格繪景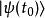 薛丁格繪景
薛丁格繪景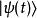 薛丁格繪景
薛丁格繪景這方程可以做這樣解釋:將時間演化算符 作用於時間是 的態矢量 ,則會得到時間是t的態矢量 。
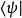 薛丁格繪景
薛丁格繪景類似地,也可以用左矢 來定義:
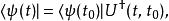 薛丁格繪景
薛丁格繪景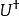 薛丁格繪景
薛丁格繪景其中,算符 是算符U的厄米共軛。
性質
么正性
由於態矢量必須滿足歸一條件,態矢量的範數不能隨時間而變:
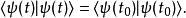 薛丁格繪景
薛丁格繪景可是,
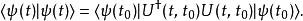 薛丁格繪景
薛丁格繪景所以,時間演化算符必須是么正算符。
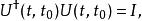 薛丁格繪景
薛丁格繪景 薛丁格繪景
薛丁格繪景其中, 是單位算符。
單位性
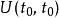 薛丁格繪景
薛丁格繪景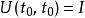 薛丁格繪景
薛丁格繪景時間演化算符 必須是單位算符 ,因為,
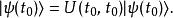 薛丁格繪景
薛丁格繪景閉包性
 薛丁格繪景
薛丁格繪景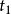 薛丁格繪景
薛丁格繪景 薛丁格繪景
薛丁格繪景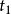 薛丁格繪景
薛丁格繪景從初始時間 到最後時間t的時間演化算符,可以視為從中途時間到最後時間t的時間演化算符,乘以從初始時間到中途時間的時間演化算符:
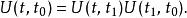 薛丁格繪景
薛丁格繪景根據時間演化算符的定義,
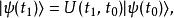 薛丁格繪景
薛丁格繪景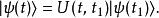 薛丁格繪景
薛丁格繪景所以
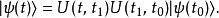 薛丁格繪景
薛丁格繪景可是,再根據定義
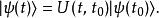 薛丁格繪景
薛丁格繪景所以,時間演化算符必須滿足閉包性:
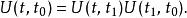 薛丁格繪景
薛丁格繪景時間演化算符的微分方程
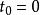 薛丁格繪景
薛丁格繪景 薛丁格繪景
薛丁格繪景 薛丁格繪景
薛丁格繪景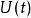 薛丁格繪景
薛丁格繪景為了方便起見,設定,初始時間永遠是0,則可忽略時間演化算符的參數,改寫為。含時薛丁格方程為
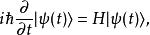 薛丁格繪景
薛丁格繪景其中,H是哈密頓量。
從時間演化算符的定義式,可以得到
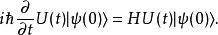 薛丁格繪景
薛丁格繪景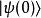 薛丁格繪景
薛丁格繪景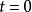 薛丁格繪景
薛丁格繪景由於可以是任意恆定態矢量(處於的態矢量),時間演化算符必須遵守方程
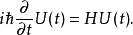 薛丁格繪景
薛丁格繪景假若哈密頓量不含時,則這方程的解答為
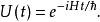 薛丁格繪景
薛丁格繪景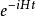 薛丁格繪景
薛丁格繪景注意到在時間t=0,時間演化算符必須約化為單位算符U(0)=I。由H是算符,指數函式必須通過其泰勒級數計算:
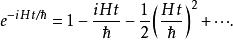 薛丁格繪景
薛丁格繪景按照時間演化算符的定義,在時間t,態矢量為
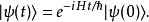 薛丁格繪景
薛丁格繪景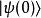 薛丁格繪景
薛丁格繪景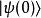 薛丁格繪景
薛丁格繪景 薛丁格繪景
薛丁格繪景注意到可以是任意態矢量。假設初始態矢量是哈密頓量的本徵態,而本徵值是,則在時間t,態矢量為
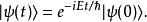 薛丁格繪景
薛丁格繪景這樣,可以看到哈密頓量的本徵態是定態,隨著時間的流易,只有相位因子在進行演化。
假設,哈密頓量與時間有關,但在不同時間的哈密頓量相互對易,則時間演化算符可以寫為
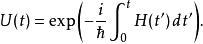 薛丁格繪景
薛丁格繪景假設,哈密頓量與時間有關,而在不同時間的哈密頓量不相互對易,則時間演化算符可以寫為
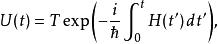 薛丁格繪景
薛丁格繪景其中,T是時間排序算符。
必須用戴森級數來表示,
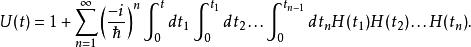 薛丁格繪景
薛丁格繪景參閱
•哈密頓-亞可比方程
