定義
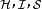 相互作用繪景
相互作用繪景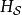 相互作用繪景
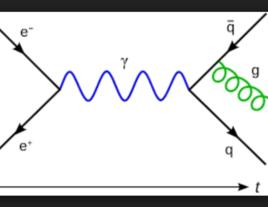
相互作用繪景為了便利分析,位於下標的符號 分別標記海森堡繪景、狄拉克繪景、薛丁格繪景。通過對於基底的一種么正變換,算符和態矢量在狄拉克繪景里的形式與在薛丁格繪景里的形式相關聯。 在量子力學裡,對於大多數案例的哈密頓量,通常無法找到薛丁格方程的精確解,只有少數案例可以找到精確解。因此,為了要能夠解析其它沒有精確解的案例,必須將薛丁格繪景里的哈密頓量分成兩個部分,
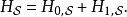 相互作用繪景
相互作用繪景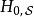 相互作用繪景
相互作用繪景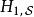 相互作用繪景
相互作用繪景其中, 有精確解,有廣泛知悉的物理行為,而 則通常沒有精確解,是對於系統的攝動。
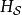 相互作用繪景
相互作用繪景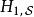 相互作用繪景
相互作用繪景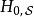 相互作用繪景
相互作用繪景假若哈密頓量 含時(例如,感受到時變外電場作用的量子系統,其哈密頓量會含時),則通常會將顯性含時部分放在 里。這樣, 不含時,而時間演化算符U(t)的公式可以簡單地表示為
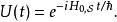 相互作用繪景
相互作用繪景其中,t是時間。
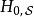 相互作用繪景
相互作用繪景假若對於某些案例, 應該設定為含時,則時間演化算符的公式會變得較為複雜:
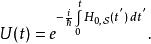 相互作用繪景
相互作用繪景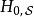 相互作用繪景
相互作用繪景本條目以下內容假設 不含時。
態矢量
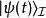 相互作用繪景
相互作用繪景在狄拉克繪景里,態矢量 定義為
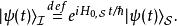 相互作用繪景
相互作用繪景 相互作用繪景
相互作用繪景其中, 是在薛丁格繪景里的態矢量。
 相互作用繪景
相互作用繪景由於在薛丁格繪景里, 態矢量 與時間的關係為
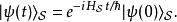 相互作用繪景
相互作用繪景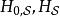 相互作用繪景
相互作用繪景所以,在 對易的條件下,可以有
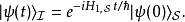 相互作用繪景
相互作用繪景算符
 相互作用繪景
相互作用繪景在狄拉克繪景里的算符 定義為
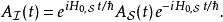 相互作用繪景
相互作用繪景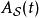 相互作用繪景
相互作用繪景其中, 是在薛丁格繪景里對應的算符。
時間演化方程
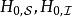 相互作用繪景
相互作用繪景 相互作用繪景
相互作用繪景以下內容,算符 都簡略標記為 。
量子態
從態矢量的定義式,可以得到態矢量對於時間的導數是
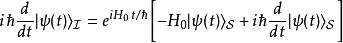 相互作用繪景
相互作用繪景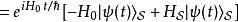 相互作用繪景
相互作用繪景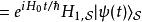 相互作用繪景
相互作用繪景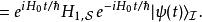 相互作用繪景
相互作用繪景將算符的定義式代入,可以得到
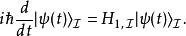 相互作用繪景
相互作用繪景這是施溫格-朝永振一郎方程的一個較為簡單的形式。
算符
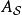 相互作用繪景
相互作用繪景 相互作用繪景
相互作用繪景假若算符 不含時,則其對應的 的時間演化為
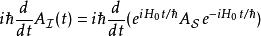 相互作用繪景
相互作用繪景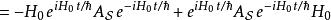 相互作用繪景
相互作用繪景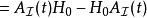 相互作用繪景
相互作用繪景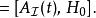 相互作用繪景
相互作用繪景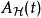 相互作用繪景
相互作用繪景這與在海森堡繪景里,算符 的時間演化類似:
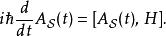 相互作用繪景
相互作用繪景密度矩陣
套用施溫格-朝永振一郎方程於密度矩陣,則可得到
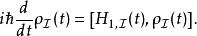 相互作用繪景
相互作用繪景各種繪景比較
各種繪景隨著時間流易會呈現出不同的演化:
| 演化 | 海森堡繪景 | 相互作用繪景 | 薛丁格繪景 |
| 右矢 | 常定 | 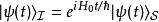 相互作用繪景 相互作用繪景 | 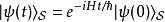 相互作用繪景 相互作用繪景 |
| 可觀察量 | 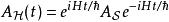 相互作用繪景 相互作用繪景 | 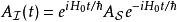 相互作用繪景 相互作用繪景 | 常定 |
| 密度算符 | 常定 | 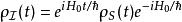 相互作用繪景 相互作用繪景 | 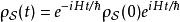 相互作用繪景 相互作用繪景 |