蒙日圓

在橢圓（雙曲線）中，任意兩條互相垂直的切線的交點都在同一個圓上，它的圓心是橢圓中心，半徑等於長半軸短半軸平方和（差）的幾何平方根，這個圓叫蒙日圓。

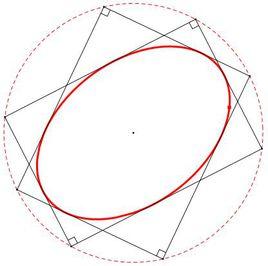
證明

方法1

設橢圓中心為O,焦點是F1,F2.焦點到中心距離為c。PM,PN是橢圓兩條切線，且互相垂直。

連OP.作OG垂直於PM,OH垂直於PN.並做F1D垂直於PM。

做F1K垂直於OG,記角OF1K=k,則

DG=F1K=c*cosk

由勾股定理，有

OG^2=OD^2-DG^2=a^2-c^2cos^2k

考慮另一焦點F2,做F2E垂直於PN,F2L垂直於OH.仿上得

OH^2=a^2-c^2sin^2k

進而得到

OP^2=OH^2+OG^2

=a^2+(a^2-c^2)

=a^2+b^2

所以OP=根號(a^2+b^2)

以上過程中的a,b,分別是長短軸半徑。

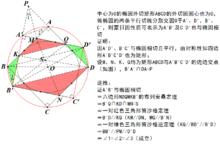方法2

方法2

（如右圖）

附：蒙日問題

蒙日圓

畫一個圓，使其與三已知圓正交.