若爾當標準型

若爾當標準型是由若干個主對角線為特徵值，下方（或上方）次對角線全為1，其餘全為0的若爾當塊按對角排列組成的準對角矩陣。不是每個n階矩陣通過初等變換都能化為對角矩陣，但每個n階複數矩陣A通過初等變換都能化為若爾當標準型，這個若爾當形矩陣除去其中若爾當塊的排列次序不同外是被矩陣A唯一確定的，它稱為矩陣A的若爾當標準型。

定義

若爾當塊

若爾當標準型

若爾當標準型

若爾當標準型

形式為的矩陣稱為若爾當塊（其中為複數）。即若當塊矩陣對角線上為相同的複數，下方（或上方）次對角線上全為1，其餘元素全為0。

若爾當標準型

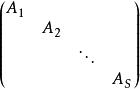若爾當標準型

若爾當標準型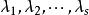

若爾當標準型

由若干個若爾當塊組成的準對角矩陣稱為若爾當標準型，其一般形狀為，其中，並且中有一些可以相等。

實例

若爾當塊實例

若爾當標準型

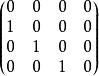若爾當標準型

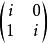若爾當標準型

例如，，都是若爾當塊。

若爾當標準型實例

若爾當標準型

若爾當標準型

若爾當標準型

若爾當標準型

例如是一個若爾當標準型矩陣。其由，，等三個若爾當塊組成。

理論推導與例子

一般採用初等因子理論來完成若爾當標準型的理論推導，其具體推導過程參見王萼芳《高等代數》346-349頁。 這裡我們採用一個具體的例子來說明若爾當標準型的計算過程。

若爾當標準型

例：求矩陣的若爾當標準型。

若爾當標準型

解：首先求的初等因子：

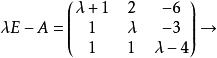若爾當標準型

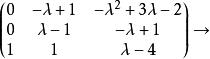若爾當標準型

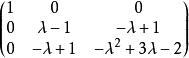若爾當標準型

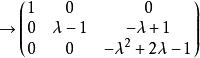若爾當標準型

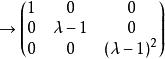若爾當標準型

。

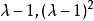若爾當標準型

因此，A的初等因子是，A的若爾當標準型是

若爾當標準型