簡介
線上性代數中， 若爾當標準型（英語：Jordan normal form）或稱 若爾當正規型（英語：Jordan canonical form）是某個線性映射在有限維向量空間上的特別的矩陣表達形式，稱作若爾當矩陣(Jordan matrix)，這矩陣接近對角矩陣：除了主對角線和主對角線上方元素之外，其餘都是零且主對角線上方的對角線的係數若不為零隻能為1，且這1左方和下方的係數（都在主對角線上）有相同的值。
定義
一個 n× n的矩陣M是可對角化的，若且唯若M滿足下列條件之一：
•M有n個線性無關的特徵向量。或者說，M有一個由特徵向量組成的基。（稱作極大無關條件）
•M的所有特徵值的幾何重數（即相應特徵子空間的維數）等於相應的代數重數。
•M的極小多項式經標準分解後，每一項都是一次項，且重數都是1。（稱作互異單根條件）
矩陣的對角化使得研究其性質變為研究相應的對角矩陣的性質，而後者顯然簡單得多。由於不是所有矩陣都滿足上述三個條件之一，有的矩陣是不可對角化的，例如以下的：
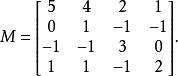若爾當分解定理。計入重數的話，M的特徵值為1, 2, 4, 4。{\displaystyle M-4I}的核的維數是1，因此M不可對角化。但經過基底變換，M相似於下面的矩陣：
若爾當分解定理。矩陣J近乎對角矩陣，除了第三列第四行係數是1。如果將後兩行和後兩列的部分作為一塊的話，矩陣J就是一個分塊對角矩陣。若爾當標準型的目標就是將更多的矩陣化簡到一類只比對角矩陣稍微複雜的矩陣：若爾當標準型。實際上這是一種簡單的分塊對角矩陣。
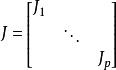若爾當分解定理。這裡的“簡單”是指每小塊矩陣都具備一種很簡單的形狀：
若爾當分解定理。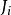
若爾當分解定理。其中主對角線上都是同一個係數，而對角線上方一排全是1。形同以上 的矩陣稱為若爾當矩陣。而矩陣J中每一個這樣的小塊被稱為 若爾當塊。
線性代數中有如下的結果：
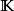若爾當分解定理。 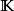若爾當分解定理。
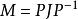若爾當分解定理。對任意係數域為 的矩陣M，只要其特徵值都在 中，就存在一個與之相似的若爾當標準型J： ，其中P是一個可逆矩陣。並且滿足：
•矩陣J的特徵值（計入重數）就是主對角線上的係數。
•對於J的一個特徵值，它的幾何重數就是屬於特徵值的若爾當塊的個數。
•所有屬於特徵值的若爾當塊的維數之和是特徵值的代數重數。
推論
•如果矩陣的係數域是一個代數閉域，那么由於其特徵值是特徵多項式的根，所以也在係數域中。於是只要係數域是一個代數閉域，所有的矩陣都相似於若爾當標準型。特別的，所有復係數矩陣都可以簡化為若爾當標準型，因為複數域是代數封閉的。
•所有的若爾當標準型都可以分解成一個對角矩陣D和一個只有對角線上一排為1的矩陣N的和。這兩個矩陣是可交換的，因為其中一個是對角矩陣。不僅如此，矩陣N是一個冪零矩陣。因此，每個相似於若爾當標準型的矩陣都可以寫成可交換的一個對角矩陣和一個冪零矩陣的和。因為與對角矩陣和冪零矩陣相似的矩陣仍然是對角矩陣和冪零矩陣。換句話說，只要一個矩陣的特徵值都在它的係數域裡（或者說它的最小多項式或特徵多項式可以分解成一次項的乘積），就可以將這個矩陣分解成一個對角矩陣和一個冪零矩陣的和，而這兩個矩陣可以交換。這個結果被稱為丹佛分解（Dunford分解），在計算矩陣的指數時很有用。
譜映射定理
用若爾當標準型以及直接的計算可以得出：如果 n× n矩陣 A的特徵值為：λ, ..., λ，那么對於多項式： p，矩陣 p( A)的特徵值是： p(λ), ..., p(λ)。
凱萊-哈密爾頓定理
凱萊-哈密爾頓定理斷言任意矩陣 A都是特徵方程的根：如果 p是 A的特徵多項式，那么 p( A) = 0。這個定理一樣可以用若爾當標準型直接計算得出。
最小多項式
方塊矩陣 A的最小多項式是使得 m( A) = 0的非常數首一多項式中次數最小者。另一種定義是：所有使得 m( A) = 0的多項式構成主理想環 C[ x]的一個理想 I，而 m則是這個理想的產生子。
對於有若爾當標準型的矩陣 A，其最小多項式以其特徵值為根，並且由若爾當標準型的形狀可以看出，每個特徵值的重數是若爾當標準型中屬於這個特徵值的最大的若爾當塊的維數。
反之已知矩陣 A的最小多項式並不能知道其若爾當標準型。要確定矩陣 A的標準型需要用到所謂的 初等因子。矩陣 A的一個初等因子是它的某一個若爾當塊的特徵多項式（或最小多項式，對於若爾當塊兩者一樣）。如果所有的初等因子都是一次多項式，那么 A可對角化。
參見
•矩陣分解
•若爾當矩陣
