概念
阿達馬因子分解定理(Hadamard factorization theorem)是有窮級整函式的一種表示式。若函式f(z)是有窮級整函式，其級為ρ，則：
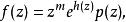阿達馬因子分解定理其中p(z)是f(z)的零點的典範乘積，h(z)是次數不超過ρ的多項式，m是f(z)在原點的零點的級。
整函式
在平面的有限部分沒有奇點的函式，例如多項式e ，sinz，cosz等，粗略地說，它們相當於初等實函式的類似物。
整函式是十分重要的一種單值複函數，許多數學家對它進行了深入研究。在這方面的第一個重要結果屬於法國數學家柯西，他在1844年證明了每一個有界的整函式是一個常數。後來人們常把這個定理歸於劉維爾，因為他在1847年也發表了這個定理。外爾斯特拉斯把實多項式分解為線性因式的定理推廣到整函式，大約在1840年，他就得到了整函式的因式分解定理(1876年發表)。1879年，法國數學家皮卡建立了整函式取值範圍的重要定理。稍後，法國數學家拉蓋爾引進了整函式的格的概念，在某種意義上，它類似於多項式的次數。1883年，龐加萊建立了整函式的模與其格的關係的定理。阿達馬研究了與此相反的問題，他在1896年給出了由函式f(z)的最大模的某種界來作出函式零點數的某種上界的估計。1897年，E.波萊爾引入函式增長級的概念，這是度量函式最大模增長速度的特徵量，在整函式理論中起著重要作用。
19世紀末，E.波萊爾綜合和改進了皮卡、龐加萊和阿達馬的工作，開始形成整函式值分布論。
全純函式
全純函式即為解析函式。能局部展成冪級數的函式，它是複變函數論研究的主要對象。解析函式類包括了數學及其在自然科學和技術套用中所遇到的大多數函式，這類函式關於算術、代數和分析的各種基本運算是封閉的，解析函式在其自然存在的域中代表唯一的一個函式，因此，對解析函式的研究具有特殊的重要性。
對解析函式的系統研究開始於18世紀。歐拉在這方面做出許多貢獻。拉格朗日最早希望建立系統的解析函式理論，他曾試圖利用冪級數的工具來發展這種理論，但未獲成功。
法國數學家柯西以他自己的工作被公認為是解析函式理論的奠基者。1814年他定義正則函式為導數存在且連續，他批判了過去許多錯誤的結果，創立了若干法則，以保證級數運算的可靠性。1825年他得到了著名的柯西積分定理，隨後又建立了柯西積分公式。柯西利用這些工具得到了正則函式在它的定義域內處處可表為收斂的冪級數的結果，其逆命題亦真。所以解析和正則是等價的。後來黎曼對柯西的工作做出了重要的發展。1900年，法國數學家古爾薩改善了正則函式的定義，只要求函式在定義域中處處有導數。
外爾斯特拉斯以冪級數為出發點開展對解析函式的研究。他定義正則函式為可以展開為冪級數的函式，創立了解析開拓理論，並利用解析開拓定義完全解析函式。柯西的方法限於研究完全解析函式的所謂單值分支，必須通過解析開拓才能和外爾斯特拉斯的理論統一起來。
阿達馬
法國數學家。生於凡爾賽，卒於巴黎。早年攻讀於巴黎高等師範學校，1892年獲理學博士學位。先後在比豐中學、波爾多理學院、巴黎大學、巴黎綜合工科學校和中央技術大學任教。他在法蘭西學院創辦了一個重要的討論班。1912年當選為巴黎科學院院士，他還是美國、英國、原蘇聯等許多國家科學機構的成員和許多大學的名譽博士。阿達馬早期的重要貢獻在解析函式論，特別是泰勒級數的解析延拓理論方面，他在1892年的論文中，第一次把集合論引進複變函數論，得到許多重要結果，成為函式論的基礎。他的《泰勒級數及其解析延拓》(1901)有很大影響。他進一步研究ζ函式，解決了長期未果的素數分布問題(1896)，從而奠定了解析數論的基礎。在偏微分方程方面，他給出了適定問題的提法。他認為，對於拉普拉斯方程，狄利克雷問題是適定的;而對於雙曲型方程，柯西問題則是適定的。他還建立了基本解的概念，明確了定解問題的涵義。他提出的發散積分的有限部分對解柯西問題有重要意義。阿達馬對泛函分析也有重要貢獻，他的《變分法教程》(1910)奠定了泛函分析的基礎，其中建議以“泛函”一詞來代替“線函式”，特別給出了用弧段上的連續函式所定義的線性泛函的一般表達式，成為里斯基本公式的先導。阿達馬的工作遍及數學的許多分支，他的初等數學講義在法國中學也頗為流行。1936年，阿達馬曾應邀來中國清華大學講學三個月。其代表作還有《數學領域中的發明心理學》(1959)。他的最後一部著作《偏微分方程論》在1964年譯成中文，由科學出版社出版。
