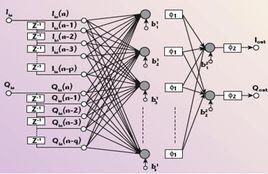
定義
在社會科學研究中,調查得來的數據往往具有層次結構( 嵌套結構)的特點。在教育學與心理學的研究中這種情況尤為常見,如關於學業成績影響因素的研究中,我們可以考慮的預測變數有學生的入學成績、學生性別、學生的社會經濟地位、班級人數、班主任和任課教師、教室環境等,這些變數中有的是學生個體層面的變數,有的是班級層面的變數。這樣的數據具有兩個水平,第一水平是學生,第二水平是班級,學生嵌套於到級之中,稱之為分層數據。
特徵
對於多層數據,傳統的回歸分析有兩種處理方法:
(1)將所有的更高一層的變數都看做是第一水平的 變數,直接在學生個體水平上對數據進行分析。這樣做存在的問題是,班級變數對同一個班級內的學生有相同的影響,不同班級學生對應不同的班級變數,而不區分班級對學生的影響,假設同一班級的學生間相互獨立是不合理的,同樣對不同班級的學生和相同班級的學生作同一假設也是不合理的。
(2)將第一水平的觀測直接合併為第二水平的觀測,然後直接對班級作分析,這樣做的主要問題是丟失了班級內學生個體間的差異的信息,而在實際中,這一部分的變異有可能占總變異中很大的一部分。
上述兩種方法有可能得到不同的結果,在對結果的解釋上也很不一致。基於上述的討論,這兩種分析數據的方法有一個共同點:它們都沒有考慮數據間分層的特點,有可能對數據結果作出不合理的甚至是錯誤的解釋。這就是傳統回歸分析方法在分析具有結構層次特點數據時的局限性。
傳統的線性回歸模型假設變數間存在直線關係,變數總體上服從常態分配,方差齊性,個體間隨機誤差相互獨立。前兩個假設較易保證,但方差齊性,尤其是個體間隨機誤差相互獨立的假設卻很難滿足。即不同班級的學生可以假設相互獨立,但是同一班級的學生由於受相同班級變數的影響,很難保證相互獨立。
因此在分析具有層次結構特點的數據時,應將傳統回歸分析中的誤差分解為兩部分,一部分是第一水平個體間差異帶來的誤差,另一部分是第二水平班級的差異帶來的誤差。可以假設第一水平個體間的測量誤差相互獨立,第二水平班級帶來的誤差在不同班級之間相互獨立。
 多層線性模型
多層線性模型多水平分析法同時考慮到不同水平的變異,這也正是多層線性分析法的套用越來越受重視的原因,它不僅在模型的假設上與實際情況更加吻合,更重要的是由這種方法得到的結果能更合理、正確地揭示事物之間的真正關係。