基本概念
線性系統
線性系統是指同時滿足疊加性與均勻性(又稱為其次性)的系統。所謂疊加性是指當幾個輸入信號共同作用於系統時,總的輸出等於每個輸入單獨作用時產生的輸出之和;均勻性是指當輸入信號增大若干倍時,輸出也相應增大同樣的倍數。對於線性連續控制系統,可以用線性的微分方程來表示。不滿足疊加性和均勻性的系統即為非線性系統。
由於線性系統較容易處理,許多時候會將系統理想化或簡化為線性系統。線性系統常套用在自動控制理論、信號處理及電信上。像無線通訊訊號在介質中的傳播就可以用線性系統來模擬。
變參數系統
根據系統是否含有參數隨時間變化的元件,自動控制系統可分為時變系統與定常系統兩大類。
定常系統又稱為時不變系統,其特點是: 描述系統運動的微分或差分方程,其係數均為常數;在物理上它代表結構和參數都不隨時間變化的這一類系統;反映在系統特性上,系統的回響特性只取決於輸入信號的形狀和系統的特性,而與輸入信號施加的時刻無關。若系統在輸入r(t)作用下的回響為y(t) ,當輸入延遲一時間τ,則系統的回響也延遲同一時間τ且形狀保持不變。定常系統的這種基本特性給分析研究帶來了很大的方便。
如果系統的參數或結構是隨時間而變化的,則稱為時變系統,也稱為變參數系統。例如火箭或帶鋼捲筒控制系統,在運行過程中隨著燃料不斷地消耗或捲筒卷繞帶鋼後直徑的變化,使得系統的質量或慣性隨時間而變化,故它們屬於時變系統。 時變系統的特點是: 由於系統的參數或結構是隨時間變化的,描述系統運動的方程為時變方程;反映在特性上,系統的回響特性不僅取決於輸入信號的形狀和系統的特性,而且還與輸入信號施加的時刻有關,這給系統的分析研究帶來了困難。
在自動控制理論中內容豐富且便於實用的是定常系統部分,而時變系統理論尚不夠成熟。雖然嚴格說來,在運行過程中由於各種因素的作用,要使實際系統的參數完全不變是不可能的,定常系統只是時變系統的一種理想化模型。但是,只要參數的時變過程比之系統的運動過程慢得多,則用定常系統來描述實際系統所造成的誤差就很小,這在工程上是容許的。
系統介紹
簡介
線性變係數系統也稱為線性時變系統。其特點是,表征系統動態過程的線性微分方程或差分方程中,至少包含一個參數為隨時間變化的函式。在現實世界中,由於系統外部和內部的原因,參數的變化是不可避免的,因此嚴格地說幾乎所有系統都屬於時變系統的範疇。但是,從研究的角度,只要參數隨時間的變化遠慢於系統狀態隨時間的變化,那么就可將系統按時不變系統來研究,由此而導致的誤差完全可達到忽略不計的程度。
線性時不變系統和線性時變系統在系統描述上的這種區別,既決定了兩者在運動狀態特性上的實質性差別,也決定了兩者在分析和綜合方法的複雜程度上的重要差別。事實上,比之線性時不變系統,對線性時變系統的研究要遠為複雜得多,也遠為不成熟得多。
對於線性系統,通常還可進一步分為線性時不變系統和線性時變系統。
線性時不變系統
線性時不變系統也稱為線性定常系統或線性常係數係數,其特點是,描述系統動態過程的線性微分方程或差分方程中,每個係數都不隨時間變化的常數。從實際的觀點而言,線性時不變系統也是實際系統的一種理想化模型,實質上是對實際系統經過近似化和工程化處理後所導出的一類理想化系統。但是,由於線性時不變系統在研究上的簡便性和基礎性,並且為數很多的實際系統都可以在一定範圍內足夠精確地用線性時不變系統來代表,因此自然地成為線性系統理論中的主要研究對象。
表示
狀態方程
n維線性時變系統的狀態方程為:
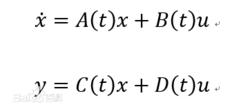 線性變參數系統
線性變參數系統其中,u是p維輸入向量,y是q維輸出向量。A、B、C、D分別是線性系統的參數,均是時間t的函式,即參數隨時間的變化 變化。
結構圖
線性時變系統的結構圖如下:
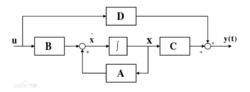 線性變參數系統
線性變參數系統特性
能控性
對於線性時變系統,當t0時刻其x值為x0,在定義時間[t0,t1]時間內,狀態完全能控的充要條件是Gram矩陣
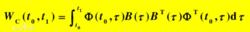 線性變參數系統
線性變參數系統非奇異。式中Φ(t,t0)為時變系統狀態轉移矩陣。
推論1(秩判據):
假設矩陣A(t)和B(t)都是n-1此連續可微的,在時間區間[t0,t1]上,若有
 線性變參數系統
線性變參數系統則系統狀態完全能控,其中分塊矩陣
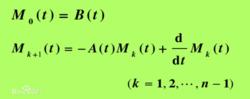 線性變參數系統
線性變參數系統推論2(秩判據):
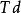 線性變參數系統
線性變參數系統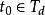 線性變參數系統
線性變參數系統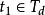 線性變參數系統
線性變參數系統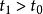 線性變參數系統
線性變參數系統假設矩陣A(t)和B(t)都是n-1此連續可微的,在時間區間 上是n-1次連續可微的,若對初始時刻 ,存在有限時刻 , ,使得
 線性變參數系統
線性變參數系統則系統在時刻t0是狀態完全能控的,其中分塊矩陣
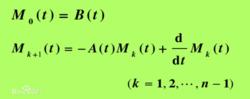 線性變參數系統
線性變參數系統能觀性
線性時變系統
 線性變參數系統
線性變參數系統在定義時間[t0,t1]時間內,狀態完全能觀的充要條件是Gram矩陣
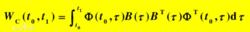 線性變參數系統
線性變參數系統為非奇異。
推論1(秩判據):
假設矩陣A(t)和C(t)都是n-1次連續可微的,在時間區間[t0,t1]上,又有
 線性變參數系統
線性變參數系統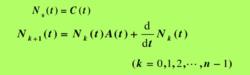 線性變參數系統
線性變參數系統則系統是狀態完全能觀的,其中分塊矩陣
推論2(秩判據):
 線性變參數系統
線性變參數系統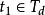 線性變參數系統
線性變參數系統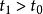 線性變參數系統
線性變參數系統對於連續時間線性時變系統,假設矩陣A(t)和C(t)都是n-1階連續可導的函式矩陣,則系統在時刻t0狀態完全能觀的充要條件為:在一個有限時刻 , 使得
則系統是狀態完全能觀的,其中分塊矩陣
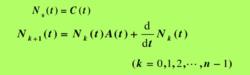 線性變參數系統
線性變參數系統穩定性
穩定性是設計控制系統的最基本要求。
線性時變系統方程:
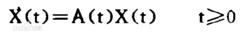 線性變參數系統
線性變參數系統如果已經求出矩陣A(t)的所有特徵值,系統漸近穩定的充要條件是:A(t)的所的特徵值都位於S的左半平面。
