定義
定義 設W是域P上的線性空間V的一個非空子集合，若對於V中的加法及域P與V的純量乘法構成域P上的一個線性空間，則稱W為V的 線性子空間（或向量子空間），或簡稱 子空間。
註：1.V的非空子集W是子空間的充分必要條件是：
（1）子集合W的任意兩個向量α與β之和α+β仍是W中的向量；
（2）域P的任一數k與子集合W的任意一個向量α的積kα仍是W中的向量。
2.線上性空間中，由單個的零向量所組成的子集合是一個線性子空間，它叫做 零子空間。
3.線性空間V自身與單獨一個零向量都是V的線性子空間。這兩個特殊的子空間稱為V的 平凡子空間；除平凡子空間外的線性子空間稱為V的 非平凡子空間。
舉例
例1 設域是 R，向量空間 V是歐幾里得空間。 取 W為最後的分量是 0 的 V中所有向量的集合。則 W是 V的子空間。
證明：顯然W非空，且
給定W中u和v，它們可以表達為u= (u,u,0) 和v= (v,v,0)。則u+v= (u+v,u+v,0+0)= (u+v,u+v,0)。因此u+v也是W的元素。
給定W中u和R中標量c，如果u= (u,u,0)，則cu= (cu,cu,c0)= (cu,cu,0)。因此cu也 是W的元素。
1.給定W中u和v，它們可以表達為u= (u,u,0) 和v= (v,v,0)。則u+v= (u+v,u+v,0+0)= (u+v,u+v,0)。因此u+v也是W的元素。
2.給定W中u和R中標量c，如果u= (u,u,0)，則cu= (cu,cu,c0)= (cu,cu,0)。因此cu也 是W的元素。
例2 設域是 R，向量空間V是是歐幾里得空間。取 W為V的使得 x= y的所有點 ( x, y) 的集合。則 W是 R的子空間。
證明：顯然W非空，且
設p= (p,p) 且q= (q,q) 是W的元素，就是說，在平面上的點使得p=p且q=q。則p+q= (p+q,p+q)；因為p=p且q=q，則p+q=p+q，所以p+q是W的元素。
設p=(p,p) 是W的元素，就是在平面中點使得p=p，並設c是R中的標量。則cp= (cp,cp)；因為p=p，則cp=cp，所以cp是W的元素。
1.p
2.p
例3 在全體實函式組成的空間中，所有的實係數多項式組成一個子空間。
例4 P[x]是（次數小於n的多項式全體）是線性空間P[x]的子空間。
性質
如果V，V是線性線性空間V的兩個子空間，那么它們的交V∩V也是V的子空間。
如果V，V是線性線性空間V的兩個子空間，那么它們的和V+V也是V的子空間。
設V，V，W都是子空間，有
1.如果V，V是線性線性空間V的兩個子空間，那么它們的交V∩V也是V的子空間。
2.如果V，V是線性線性空間V的兩個子空間，那么它們的和V+V也是V的子空間。
3.設V，V，W都是子空間，有
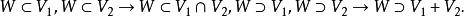線性子空間4.對於子空間V，V2以下三個論斷是等價的：
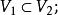線性子空間1）
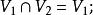線性子空間2）
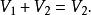線性子空間3）
5（維數公式）如果V，V是線性空間V的兩個子空間，那么：維（V）+維（V）=維（V+V）+維（V∩V）.
6.如果n維線性空間V中兩個子空間V，V的維數之和大於n，那么V，V必含有非零的公共向量。
7.設U是線性空間V的一個子空間，那么一定存在一個子空間W使V等於U與W的直和。
