簡介
閉線性子空間是一類子空間。
賦范空間中的按範數導出的距離還是閉的線性子空間稱為閉線性子空間。
線性子空間
設W是域P上的線性空間V的一個非空子集合,若對於V中的加法及域P與V的純量乘法構成域P上的一個線性空間,則稱W為V的 線性子空間(或向量子空間),或簡稱 子空間。
註:1.V的非空子集W是子空間的充分必要條件是:
(1)子集合W的任意兩個向量α與β之和α+β仍是W中的向量;
(2)域P的任一數k與子集合W的任意一個向量α的積kα仍是W中的向量。
賦范空間
 閉線性子空間
閉線性子空間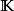 閉線性子空間
閉線性子空間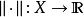 閉線性子空間
閉線性子空間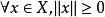 閉線性子空間
閉線性子空間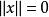 閉線性子空間
閉線性子空間 閉線性子空間
閉線性子空間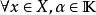 閉線性子空間
閉線性子空間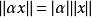 閉線性子空間
閉線性子空間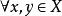 閉線性子空間
閉線性子空間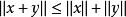 閉線性子空間
閉線性子空間 閉線性子空間
閉線性子空間 閉線性子空間
閉線性子空間 閉線性子空間
閉線性子空間 閉線性子空間
閉線性子空間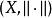 閉線性子空間
閉線性子空間 閉線性子空間
閉線性子空間向量的範數是長度概念的推廣。設
是域(實數域或複數域)上的線性空間,函式滿足條件:1)對;且若且唯若;
2)對,有(齊次性);
3)對,有(三角不等式)。
稱是上的一個範數,上定義了範數稱為(線性)賦范空間,記為,有時簡記為。
