相關內容
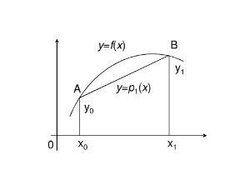
線性內插法是指兩個量之間如果存線上性關係,若A(X1,Y1),B(X2,Y2)為這條直
線上的兩個點,已知另一點P 的Y0 值,那么利用他們的線性關係即可求得P 點的對應值X0。通常套用的
是點P 位於點A、B 之間,故稱“線性內插法”。在求解X0 時,可以根據下面方程計算:
(X0- X1)/(X2 - X1)= (Y0- Y1)/(Y2 - Y1)。
在具體套用中,關鍵是要搞清楚6 個量X1,Y1,X2,Y2,X0,Y0 之間的關係。
(1)“內插法”的原理是根據等比關係建立一個方程,然後解方程計算得出所要求的數據。
(2)仔細觀察方程會看出一個特點,即相對應的數據在等式兩方的位置相同。例如:X1 位於等式左方
表達式的分子和分母的右側,與其對應的數字Y1 應位於等式右方的表達式的分子和分母的右側。
(3)應該注意的是,如果對X1 和X2 的數值進行交換,則必須同時對Y1 和Y2 的數值也交換,否則,計
算結果一定不正確。總的原則是直線上任意兩點間的變數X 差值之比應等於對應的變數Y 的差值之比。
內插法在財務管理[2,3],投資決策[4- 6],古代曆法[7]等領域都有廣泛的套用.
舉個例子,已知X1=1時Y1=3,X3=3時Y3=9,那么x=2時用線性插值得到y就是3和9的算術平均數6。