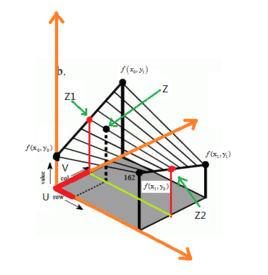
示例
已知的紅色數據點與待插值得到的綠色點
假如我們想得到未知函式 f在點 P= ( x, y) 的值，假設我們已知函式 f在 Q11 = ( x1, y1)、 Q12 = ( x1, y2), Q21 = ( x2, y1) 以及 Q22 = ( x2, y2) 四個點的值。
首先在 x方向進行線性插值，得到R1和R2，然後在 y方向進行線性插值，得到P.
這樣就得到所要的結果 f( x, y).
其中紅色點Q11,Q12,Q21,Q22為已知的4個像素點.
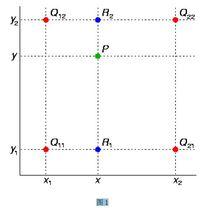雙線性插值第一步：X方向的線性插值，在Q12,Q22中插入藍色點R2，Q11，Q21中插入藍色點R1；
第二步 ：Y方向的線性插值 ,通過第一步計算出的R1與R2在y方向上插值計算出P點。
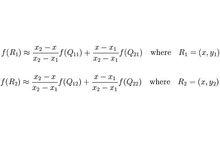x方向上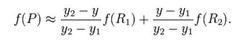
雙線性插值線性插值的結果與插值的順序無關。首先進行 y方向的插值，然後進行 x方向的插值，所得到的結果是一樣的。雙線性插值的結果與先進行哪個方向的插值無關。
如果選擇一個坐標系統使得 的四個已知點坐標分別為 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以化簡為
f(x,y)=f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xy
在x與y方向上，z值成單調性特性的套用中，此種方法可以做外插運算，即可以求解Q1~Q4所構成的正方形以外的點的值。
雙線性插值的一個顯然的三維空間延伸是三線性插值。
三線性插值的方法可參看matlab中的interp3
特點
當對相鄰四個像素點採用雙線性插值時，所得表面在鄰域處是吻合的，但斜率不吻合。並且雙線性灰度插值的平滑作用可能使得圖像的細節產生退化，這種現象在進行圖像放大時尤其明顯。
雙線性插值