定理定義
緊性定理(compactness theorem)是在解的先驗估計及解的存在性問題研究中起重要作用的定理。設A∈OPS(Ω),0≤δ<ρ≤1,分布核K具緊支集,若A的象徵σ滿足條件:
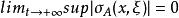 緊性定理
緊性定理則A可延拓為L²(Ω)→L²(Ω)的緊運算元。
在邏輯數學中,緊性定理表明,若且唯若每個有限子集具有模型時,一階句子的集合具有模型。 這個定理是模型理論中的一個重要工具,因為它提供了用於構建有限一致的任何一組句子的模型的一種有用的方法。
命題演算的緊性定理是Tychonoff定理(表示緊湊空間的乘積是緊湊的)套用於緊性的斯通空間得到的結果;因此定理的名稱是緊性定理。它類似於在拓撲空間中的緊湊性的有限相交特性表征:如果每個有限子集具有非空交集,則緊湊空間中的閉集的集合具有非空交集。
緊性定理和Löwenheim-Skolem定理是Lindström定理在一階邏輯中套用的兩個關鍵定理。 雖然對於非一階邏輯有一些簡潔的緊性定理,但緊性定理本身並不適用於一階邏輯。
庫爾特·戈德爾(KurtGödel)在1930年證明了可數的緊性定理。阿拉托·馬爾塞夫(Anatoly Maltsev)在1936年證明了不可數的定理形式。
先驗估計
先驗估計是近代研究偏微分方程的一種基本方法和技巧。對偏微分方程定解問題,在解存在的假設下,通過方程係數、自由項及定解條件估計解在某個巴拿赫空間(一般是索伯列夫空間或連續可微函式空間)中的範數的上界的不等式,例子參見“紹德爾估計”、“解的L估計”。利用先驗估計來探討偏微分方程定解問題解的存在、惟一及光滑等性質是近代偏微分方程研究的一個重要方法。
定理套用
緊性定理在模型理論中有很多套用,這裡列舉幾個典型的套用。
套用一
緊性定理意味著羅賓遜原則:如果一階句子在特徵零的每個場中都存在,則存在一個常數p,使得每個特徵大於p的場都保持該句子。這可以看出如下:假設φ是在特徵零的每個場中保持的句子。那么它的否定¬,連同場公理和句子1 + 1≠0,1 + 1 + 1≠0,...的無限序列是不可滿足的(因為沒有¬保持的特徵0的場,並且無限序列的句子確保任何模型將是特徵0的場。因此,這些句子的有限子集A是不可滿足的。我們可以假設A包含¬φ,欄位公理,對於某些k,形式1 + 1 + ... + 1≠0的第一個k個句子(因為添加更多的句子不會改變不滿足)。讓B包含除了¬φ之外的所有句子。那么具有大於k的特徵的任何場是B的模型,並且¬與B一起是不可滿足的。這意味著φ必須保持在B的每一個模型中,這意味著φ在每個特徵大於k的場中都是正確的。
套用二
緊性定理的第二個套用表明,任何具有任意大的有限模型的理論或單一的無限模型都具有任意大基數的模型(這是上升的Löwenheim-Skolem定理)。所以,例如,有一些非標準的Peano算法模型,其數量很多是很自然的。為了達到這個目的,令T為初始理論,令k為任何基數。添加到κ的每個元素的T一個常數符號的語言。然後添加到T的句子集合,表示從新集合中任何兩個不同的常量符號表示的對象是不同的(這是一個κ2句子的集合)。由於這個新理論的每個有限子集都可以通過足夠大的T的有限模型或任何無限模型來滿足,整個擴展理論是可以滿足的。但擴展理論的任何模型至少具有k的基數。
套用三
緊性定理的第三個套用是實數的非標準模型的構建,即包含“無窮小”數字的實數理論的一致擴展。為了看到這一點,讓Σ是實數理論的一階公理化。考慮通過向語言添加新的常數符號ε並且與所有正整數n的公理ε> 0和公理ε<1 / n相鄰而獲得的理論。顯然,標準實數R是這些公理的每個有限子集的模型,因為實數滿足Σ中的所有內容,並且可以通過合適的ε選擇來滿足關於ε的公理的任何有限子集。通過緊性定理,存在滿足Σ的模型* R,並且還包含無窮小元素ε。類似的論證,相鄰的公理ω> 0,ω> 1等,表明無限大整數的存在不能被任何公理化的公理化Σ排除。
定理證明
可以使用Gödel的完整性定理來證明緊性定理,該定理確定了若且唯若沒有證據證明矛盾時,一組句子是可滿足的。由於證明總是有限的,因此僅涉及給定句子的有限許多,緊密度定理如下。事實上,緊性定理與Gödel的完整性定理相當,兩者都等價於布爾素理想定理,即選擇公理的弱形式。
Gödel最初以這種方式證明了緊性定理,但後來發現了緊性定理的一些“純粹的語義”證明,即提及真理而不是可證明性的證明。其中一個證明依賴於以下選擇的公理的結論:
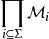 緊性定理
緊性定理證明:修正一級語言L,並且將Σ作為L句的集合,使得每個有限子集合的L個句子,它的i⊆Σ具有一個模型Mi,還要讓成為結構和I的有限子集的直積。對於I中的每一個,I讓Ai:= {j∈I:j⊇i}。
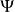 緊性定理
緊性定理現在對於Σ中的任何公式,我們有:
集合A {φ}在U中;
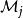 緊性定理
緊性定理每當j∈A{φ},則φ∈j,因此φ保持在中。
