基本介紹
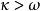 緊基數
緊基數強緊基數是一類很“大”的大基數,若對於任何無窮基數λ,語言L都是(λ,κ)緊的,且,則稱基數κ是強緊基數,語言L是(λ,ω)緊的,這兒λ是任意無窮基數,因而,強緊基數也是對無窮基數ω的某些性質進行推廣而得到的,開斯勒(H.J.Keisler)和波蘭學者塔爾斯基(A.Tarski)於1964年引入強緊基數的概念。
強緊基數必是可測基數,因而也必是弱緊基數,福平卡-赫巴契克於1966年證明了:若存在強緊基數,則對任何集合X,V≠L[X],這裡V是全集,L[X]是相對於X的可構造集,或說是從X出發的可構造集,以色列學者索洛韋(R.M.Solovay)於1974年用力迫法證明了:若κ是強緊基數,對於每個>κ的奇異強極限基數λ,有2 =λ ,亦即對於一些很特殊的、很大的基數,證明了廣義連續統假設是成立的 。
相關定義及定理
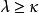 緊基數
緊基數設κ,λ為基數,,令
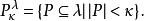 緊基數
緊基數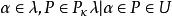 緊基數
緊基數設U是P(λ)上的濾子,若對每一個 ,則稱U是精細的(Fine)。
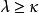 緊基數
緊基數定義1 設κ為正則不可數基數, 為任意基數,稱κ為λ-強緊的充要條件為在Pλ上存在非主的、精細的、κ-完全的超濾(或Pλ上存在精細的測度) 。
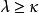 緊基數
緊基數κ稱為強緊的充要條件為對所有 ,κ是λ-強緊的。
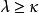 緊基數
緊基數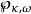 緊基數
緊基數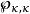 緊基數
緊基數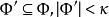 緊基數
緊基數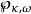 緊基數
緊基數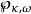 緊基數
緊基數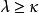 緊基數
緊基數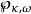 緊基數
緊基數定義 2 設κ為正則不可數基數, 為任意基數, (或 )為無窮語言,若對任意語句集Φ,|Φ|=λ,當 時,Φ’都有模型,則Φ有模型,那么稱 有(κ,λ)強緊性定理,稱 是強緊的,若對所有 , 有(κ,λ)-強緊性定理。
下列定理說明強緊來源於無窮語言的(κ,λ)一強緊性定理。
下面定理的證明請參考相應書籍 。
定理3 設κ是正則基數,則下列命題等價:
[1]對任意S,S上每一個κ-完全超子可擴充成S上的超濾;
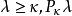 緊基數
緊基數[2]對任何 上存在精細的測度;
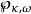 緊基數
緊基數[3]無窮語言 滿足強緊性定理。
定理4 若κ≤λ,則下列命題等價:
[1]κ是λ-強緊的.
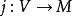 緊基數
緊基數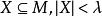 緊基數
緊基數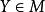 緊基數
緊基數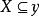 緊基數
緊基數[2]存在初等嵌入 ,以κ為臨界點,使得當 時,有 ,滿足 ,
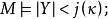 緊基數
緊基數[3]若F是集合S上的任一κ-完全的濾子,它由基數≤λ的集所生成,則F可擴充的S上的κ-完全超濾 。
推論5 強緊基數是可測基數。
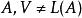 緊基數
緊基數定理6 (沃列克-赫貝西(Vopenka-Hrbacek)若存在強緊基數,則對任何 。
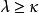 緊基數
緊基數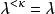 緊基數
緊基數定理7 若λ為正則基數,,κ是λ-強緊基數,則 。
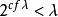 緊基數
緊基數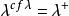 緊基數
緊基數定理8 若存在強緊基數,則在該基數以上的奇異基數,其奇異基數假定都成立(即若κ為強緊基數,λ>κ為奇異基數,則當 時有 )。
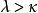 緊基數
緊基數推論9 若κ是強緊基數,為奇異強極限基數,則2 =λ 。
下面給出可測基數與強緊基數之間關係的一個性質.
定理10(梅勞斯(Menas))若κ是可測基數,並且它是強緊基數的極限,則κ是強緊基數 。
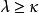 緊基數
緊基數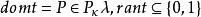 緊基數
緊基數定義11 設κ為正則基數,,函式t,使得,則稱t為生長在Pλ的元素P上的二元函式。
設M是滿足下列性質的函式族:
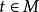 緊基數
緊基數[1]若,則t生長在Pλ元素上,
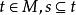 緊基數
緊基數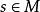 緊基數
緊基數[2]若,則,
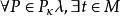 緊基數
緊基數[3](t生長在P上),
則稱M為二元(κ,λ)-網(Mess)(簡稱網)。
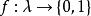 緊基數
緊基數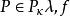 緊基數
緊基數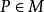 緊基數
緊基數如果存在函式,使得對每一個↑,則稱f為M的解(Solution),這時M也稱為可解的。
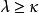 緊基數
緊基數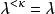 緊基數
緊基數定理12 設κ是不可及基數,,,則κ是λ-強緊的充要條件為每一個二元(κ,λ)-網可解 。

