里所碼簡介
里所碼被廣泛的套用於各種商業用途,最顯著的是在CD、DVD和藍光光碟上的使用;在數據傳輸中,它也被用於DSL和WiMAX;廣播系統中DVB和ATSC也閃現著它的身影;在計算機科學裡,它是RAID 6標準的重要成員。里所碼是定長碼。這意味著一個固定長度輸入的數據將被處理成一個固定長度的輸出數據。在最常用的(255,223)里所碼中,223個裡德-所羅門輸入符號(每個符號有8個比特)被編碼成255個輸出符號。
•大多數里所錯誤校正編碼流程是成體系的(Systematic code)。這意味著輸出的碼字中有一部分包含著輸入數據的原始形式。
•符號大小為8位的里所碼迫使碼長(編碼長度)最長為255個符號。
•標準的(255,223)里所碼可以在每個碼字中校正最多16個裡所符號的錯誤。由於每個符號事實上是8個比特,這意味著這個碼可以校正最多16個短爆發性錯誤。
里所碼如同卷積碼一樣,是一種透明碼。這代表如果信道符號在佇列的某些地方被反轉,解碼器一樣可以工作。解碼結果將是原始數據的補充。但是,里所碼在縮短後會失去透明性。在縮短了的碼中,“丟失”的比特需要被0或者1替代,這由數據是否需要補足而決定。(如果符號這時候反轉,替代的0需要變成1)。於是乎,需要在里所解碼前對數據進行強制性的偵測決定(“是”或者“補足”)。
里所碼定義
概述
在里德-所羅門數據編碼 背後的核心可以形象化的表示為多項式。這種碼依靠一個代數理論,這個代數理論說明任何k個唯一的確定點表示一個階數至少為k-1的多項式。傳送者表明一個在有限域中的k-1階的多項式,它表示k個數據點。這個多項式就根據它在各點的賦值被“編碼”,實際傳送的是這些值。在傳輸中,一些值會被破壞。所以,實際傳送的點不止k個。只要正確地接收了足量的數值,接收方就可以推算出原始多項式,進而譯出原始數據。同樣的,我們可以通過插值來修正曲線。RS碼可以將一組有錯誤序列的信息碼轉換到找回畫出原始曲線的多項式的係數。
數學公式
 里所碼
里所碼 里所碼
里所碼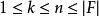 里所碼
里所碼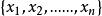 里所碼
里所碼 里所碼
里所碼給定一個有限域 和多項式環 ,令n和k滿足 ,選擇F中的n個確定元素,記作 ,碼本C是通過計算F中每個 的階數小於k的多項式得到的值,即
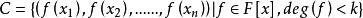 里所碼
里所碼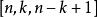 里所碼
里所碼C是 碼;換句話說,是F中長為n,維為k,最小漢明距離為n-k+1的線性碼。
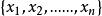 里所碼
里所碼 里所碼
里所碼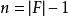 里所碼
里所碼一個RS碼滿足以上的形式,並遵循集合 是 域中所有非零元素組成的集合(因而, )。
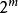 里所碼
里所碼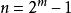 里所碼
里所碼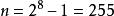 里所碼
里所碼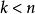 里所碼
里所碼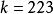 里所碼
里所碼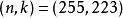 里所碼
里所碼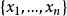 里所碼
里所碼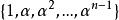 里所碼
里所碼 里所碼
里所碼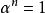 里所碼
里所碼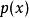 里所碼
里所碼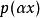 里所碼
里所碼需要注意的是:RS碼在實際套用中,常常使用一個有 個元素的有限域F。這樣,每個符號就可以表示為一個m比特的數值。傳送方以編碼塊的形式傳送數據點,編碼塊的符號數量為 個。這樣,一個用於8比特符號的RS碼每塊有 個符號。(在位元組型計算機系統普及的今天,這個數字很實用。)編碼塊中的數據符號k是一個設計參數, 。在一個n = 255的符號塊中,常用 的8比特數據符加上32個8比特校驗符來編碼,用 表示,每塊最多可以校正16個符號錯誤。由有限域中的非零元素構成的集合 可以寫作 , 是一個"單位的n次本原根"。習慣上按照這種順序對RS碼進行編碼。由於 ,並且對於每個多項式 ,函式 是與它同次的多項式,因而RS碼是循環的。
RS碼與BCH碼的關係
1968年,Berlekamp發現了一種BCH碼解碼算法。由於RS碼可以看作是BCH碼的特例,該算法也可用於解碼RS碼。
 里所碼
里所碼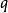 里所碼
里所碼 里所碼
里所碼 里所碼
里所碼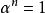 里所碼
里所碼 里所碼
里所碼 里所碼
里所碼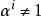 里所碼
里所碼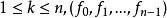 里所碼
里所碼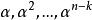 里所碼
里所碼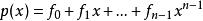 里所碼
里所碼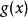 里所碼
里所碼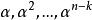 里所碼
里所碼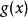 里所碼
里所碼通過RS碼的另一種定義方法,可以很容易的看出RS碼是BCH碼的一種特例。令有限域 大小為 , 為 [[n次原單位根]],亦即 ,且對所有小於 的正整數 ,均有 。給定 是RS碼的碼字若且唯若 是多項式 的根。這樣,很容易可以看出RS碼是一種多項式碼,也就是BCH碼。生成多項式 為 的最小多項式,而碼字為能夠整除多項式 的多項式 。
RS碼的兩種定義的等價性
RS碼的兩種定義方式有著非常大的區別,而它們的等價關係並不是顯而易見的。在第一種定義中,碼字是多項式的值,而在第二種定義中,碼字是多項式的係數。另外,第一種定義要求多項式具有特定的比較小的冪次,而在第二種定義中,多項式需要有特定的根。
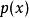 里所碼
里所碼 里所碼
里所碼 里所碼
里所碼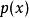 里所碼
里所碼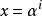 里所碼
里所碼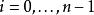 里所碼
里所碼 里所碼
里所碼 里所碼
里所碼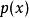 里所碼
里所碼這兩種定義的等價性可以通過有限域上的離散傅立葉變換來證明。離散傅立葉變換創建起了多項式的係數與值指間的對偶關係。這種對偶關係可以不嚴格的概述如下:令 和 為兩個次數小於 的多項式。如果多項式 的在 ( 是1的n次原單位根)處的值是 的係數,那么 在這些點上的取值在經過乘以一個特定的係數和重新排列以後就成為了 的係數。
嚴格的說,令
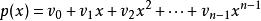 里所碼
里所碼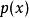 里所碼
里所碼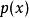 里所碼
里所碼 里所碼
里所碼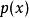 里所碼
里所碼 里所碼
里所碼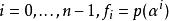 里所碼
里所碼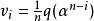 里所碼
里所碼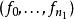 里所碼
里所碼同時假定 和 為離散傅立葉變換對,那么 和 的係數和取值有如下關係:對所有的 並且 。這樣,我們可以得出 是滿足RS碼第一種定義方式的碼字。
 里所碼
里所碼 里所碼
里所碼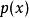 里所碼
里所碼1、若且唯若的次數小於 ( 是 的係數)
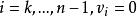 里所碼
里所碼2、若且唯若如果 ,
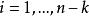 里所碼
里所碼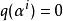 里所碼
里所碼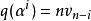 里所碼
里所碼3、若且唯若對所有的 , (由於 ),
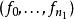 里所碼
里所碼4、若且唯若 是RS碼在第二種定義方式下的碼字。
這樣,兩種定義方式的等價性便得到了證明。
里所碼性質
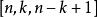 里所碼
里所碼 里所碼
里所碼 里所碼
里所碼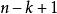 里所碼
里所碼 里所碼
里所碼 里所碼
里所碼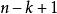 里所碼
里所碼RS碼是一個 碼,是一種定義在有限域 上的長度為{\displaystyle n},信息長度為 ,最短漢明距離為 的線性分組碼。由於這種編碼滿足Singleton界,因此它是一種最大距離可分碼。由於碼長為 信息長度為的碼的最大漢明距離為,所以在這種意義下RS碼是一種最優的編碼方法。
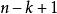 里所碼
里所碼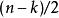 里所碼
里所碼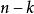 里所碼
里所碼 里所碼
里所碼 里所碼
里所碼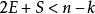 里所碼
里所碼RS碼的糾錯能力由最短漢明距離決定,為。如果預先並不知道錯誤的位置,RS碼最多可以糾正個錯誤。而在某些情況下,我們可以預知錯誤的位置(比如BEC信道),此時RS碼最多可以糾正個錯誤。如果我們可以預先知道個錯誤位置,而此外還有個未知的錯誤位置,那么在滿足的情況下,我們可以完全糾正這些錯誤 。
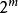 里所碼
里所碼 里所碼
里所碼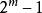 里所碼
里所碼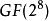 里所碼
里所碼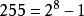 里所碼
里所碼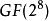 里所碼
里所碼 里所碼
里所碼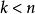 里所碼
里所碼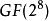 里所碼
里所碼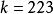 里所碼
里所碼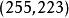 里所碼
里所碼在實際套用中,RS碼經常使用大小為的有限域。在這種情況下,每個符號都包含有比特的信息。傳送者將編碼後的分組傳送給接受者,每個分組通常含有個符號。例如,定義在上的RS碼每個分組包含有個符號。由於計算機通常以位元組為單位來處理數據,因此定義在的RS碼非常流行。設計參數需要滿足,對於定義在上的RS碼,通常選擇。這個RS碼包含有223個數據符號和32個校驗符號,表示為RS碼,它最多可以糾正16個符號錯誤。RS碼的這種性質使得它非常適合糾正傳輸系統中的突發錯誤。這是由於不論一個符號中有多少個比特發生錯誤,都只發生了一個符號錯誤。而對於不發生突發錯誤的傳輸系統,RS碼的性能通常不如普通的二元碼。
