紊流水頭損失分為兩部分,即沿程水頭損失和局部水土損失,下面分別介紹。
沿程水頭損失
沿程水頭損失公式紊流的沿程水頭損失可採用達西-魏斯巴赫公式
λ與雷諾數Re及Δ/d有關。Δ為管壁粗糙度高度,d為圓管的直徑。
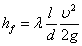
1933年德國科學家尼古拉茲在圓管內壁貼上上經過篩分具有相同粒徑(即絕對粗糙度Δ)的砂粒,製成人工均勻顆粒粗糙的管道,得出了反映圓管流動情況的試驗結果,得出了 λ=f(Re,Δ/d)的規律。尼古拉茲實驗雖然不能完全用於工業管道,但是它全面揭示了不同流態情況下 λ和雷諾數Re及相對粗糙度Δ/d的關係,從而說明確定λ的各種經驗公式和半經驗公式有一定的適用範圍。
人工粗糙管沿程阻力係數半經驗公式沿程阻力係數的半經驗公式是從研究斷面流速分布著手,綜合普朗特理論和尼古拉茲實驗結果推出的。
按照粗糙管的不同,可按下圖的公式計算:

計算時引入“當量粗糙高度”,把工業管道的粗糙折算成人工粗糙。當量粗糙高度是指和工業管道粗糙管區λ值相等的同直徑人工粗糙管的粗糙高度。
為了簡化計算,1944年莫迪在柯列布魯克公式的基礎上,繪製了工業管道λ的計算曲線,即莫迪圖,可按Re及相對粗糙度 Δ/d直接查的λ值。
1)希夫林松公式:
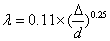
2)舍維列夫公式
3)謝才公式
局部水頭損失
工業管道中,經常在管道中間設有異徑管、三通、閘閥、彎道、格柵等部件或其他構築物。在這些局部阻礙處均勻流遭到破壞,引起流速分布的急劇變化,從而形成形狀阻力和摩擦阻力,由此產生局部水頭損失。
產生的原因邊界層分離和漩渦區得存在是造成局部水頭損失的主要原因。
過水斷面突然擴大的水頭損失計算有管徑A1到管徑A2過水斷面突然擴大,其水頭損失計算公式如下:
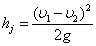
沿程水頭損失實例計算
已知鑄鐵管直徑d=25cm,長為700m,通過流量為56L/s,水溫為10C°,求水頭損失。
解:計算過程以及結果如下圖所示

