計算方法
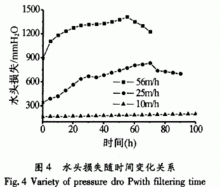
曲線1單位重量的水或其他液體在流動過程中因克服水流阻力作功而損失的機械能，具有長度因次。水頭損失可分為沿程水頭損失hf及局部水頭損失hj兩類。某流段的總水頭損失hw為各分段的沿程水頭損失與沿程各種局部水頭損失的總和
沿程水頭損失
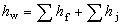公式1克服沿程摩擦阻力作功而損失的水頭，它隨著流程長度而增加。恆定均勻管流沿程水頭損失的達西－魏斯巴赫公式
式中g為重力加速度；d、l、v為管道直徑、 流段長
度、斷面平均流速；λ為無因次係數,稱為沿程摩阻係數。式(2)亦適用於明渠水流，式中管徑d須代以明渠水力半徑R（見謝才公式）的4倍。德國學者J.尼庫拉德塞曾用人工砂粒粗糙的辦法進行系統試驗, 結果繪成以1g(100λ)及lgRe(雷諾數 ，ν為液體運動粘滯係數)為縱橫坐標,以相對粗糙度r0/κs(r0為圓管半徑,κs為砂粒粗糙高度)為參數的曲線圖。圖中ɑb線代表層流區， 。c以右為紊流區,又可分為三個流區：①光滑區(cd線), λ=f(Re)；②完全粗糙區(ef線以右的B區)屬充分發展了的紊流, , ,又稱阻力平方區;③過渡粗糙區(cd、ef線間的A區),λ=f(Re,κs/r0)。b、c之間為層流轉變為紊流的過渡區，試驗點子亂，範圍狹窄，一般可作紊流對待。b點，Re≈2300；c點Re≈4000。明渠均勻流的λ值也有類似的變化規律。
水頭損失
工程界習慣沿用一些經驗公式和圖表計算沿程水頭損失。明渠流實際上多屬阻力平方區，廣泛採用謝才公式和曼寧公式。
參數圖局部水頭損失
儀器在流動局部地區因邊界急局改變引起流動急劇調整、消耗能量而損失的水頭。管渠中進水口、彎段、門槽、斷面突然擴大或突然收縮，管道中設定閥門、接頭或其他配件，常引起流動分離並發生鏇渦。鏇渦的形成與衰減及流速分布的急劇改變均會消耗液體機械能。高雷諾數下的水流試驗表明，局部水頭損失近似地與該局部地區的特徵流速水頭成正比，即：
(3)
計算公式局部水頭損失係數ζ的大小基本上取決於流動的幾何條件，如斷面急劇改變前後的面積比，彎管相對曲率半徑，閥門的形狀和尺寸等，ζ值由實驗測定。低雷諾數流動的ζ值不僅與流動幾何條件而且與流動狀態(Re值)有關。
水頭損失