定義
一個多面體,如果滿足下列條件,就叫做 簡單多面體:
(1) 各面都是簡單多邊形;
(2) 多面體的棱彼此之間、棱與面的內部都沒有公共點;
(3) 多面體的各頂不附著於各面的內部或各棱之上;
(4) 多面體上共有一頂的一切面角,圍拱著這個頂只構成一個多面角。
對於多面體,如果它們經過拓撲變換可變為球面,那么它們都是簡單多面體。
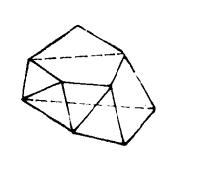 圖1
圖1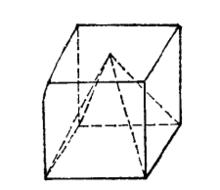 圖2
圖2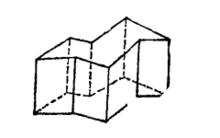 圖3
圖3圖1是一個簡單多面體,圖2所示的多面體不是簡單多面體,因為它的一個頂點附著在多面體的一個面內。圖3所示多面體是由八個矩形和兩個凹八邊形組成的十面體,它也是個簡單多面體。
特別需要指出的是,所有凸多面體都是簡單多面體 。
歐拉定理
簡單多面體的頂點數V,面數F,棱數E,恆有下面的關係式:
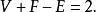 簡單多面體
簡單多面體證明: 將簡單多面體的一個面去掉,構想它是橡皮膜上畫著的,這樣可以攤在平面上,成一平面圖形,這個過程中,頂點數V,棱數E均未改變,只是面數減少1記為F因此要證簡單多面體有V+F-E = 2,只要對相應的平面網路證V+F-E =1即可。
(1) 去掉一條棱,除去一個圈,因而減少一個面。頂點數不發生變化。所以V+F-E的值不變,直到把所有的圈都除掉為止,網路變成一棵樹。這時V+F-E值仍保持不變。
(2) 從所剩的樹中去掉一個葉子,就減去一個頂點,減少一條邊,此時V+F-E仍保持不變,到最後只剩下兩個頂點一條邊,V+F-E仍保持不變,但此時V= 2,F=0,E=1,V+F-E=2+0-1=1。
所以:V+F-E =1+1= 2。
歐拉定理揭示了簡單多面體的頂點數、面數、棱數存在著的關係:V+F-E = 2。常數2是簡單多面體經過拓撲變換下的不變數。它是一個與通常的長度、角度、面積、體積等度量無關的數。
歐拉定理(或歐拉公式)是拓撲學中的一個重要公式,在初等幾何中對於討論凸多面體的頂數、棱數、面數的有關命題十分重要。
為了便於敘述,我們把簡單多面體的頂點數、面數、棱數分別記為V、F、E,其三面角、四面角、五面角...的頂點數依次記為V,V,V,...其面上的三角形、四邊形、五邊形...的面數,依次記為F,F,F,...。
顯然有:
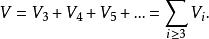 簡單多面體
簡單多面體命題1
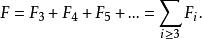 簡單多面體
簡單多面體命題2
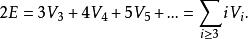 簡單多面體
簡單多面體命題3
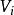 簡單多面體
簡單多面體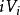 簡單多面體
簡單多面體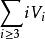 簡單多面體
簡單多面體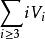 簡單多面體
簡單多面體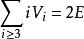 簡單多面體
簡單多面體證明:由於 為i 面角的頂數, 為從各個i 面角的頂點發出的棱數之和,而 為從各個頂點發出的棱數的總和,在 中,每條棱均從兩個頂點發出,因而每條棱都被計算了兩次,則 。
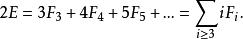 簡單多面體
簡單多面體命題4
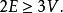 簡單多面體
簡單多面體命題5
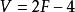 簡單多面體
簡單多面體命題6 設一個簡單多面體的多面角都是三面角,則 。
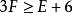 簡單多面體
簡單多面體命題7 在凸面體中,有 。
定理 空間僅存五種正多面體 。
多面體的有關知識
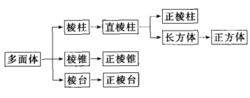 圖4
圖41. 簡單多面體的基礎知識包括稜柱、稜錐的概念、性質、側面積、表面積、截面積、體積的計算。簡單旋轉體的基礎知識包括圓柱、圓錐、球的表面積、體積計算。簡單多面體的分類,正多面體的性質等知識。
2. 以柱、錐和特殊簡單多面體為載體的立體幾何綜合型問題研究既要運用線面關係的判定定理、性質定理,又要運用其基本性質。
3. 簡單幾何體面積與體積計算。側面積和體積的計算首先要熟記公式,並能用函式的觀點去理解柱、錐、球的面積公式和體積公式,理解其變化規律 。
多面體的有關概念
(1) 多面體:由若干個平面多邊形圍成的空間圖形叫做多面體。
(2) 凸多面體:把一個多面體的任何一個面伸展成平面,如果其餘各面都位於這個平面的同一側,這樣的多面體叫做凸多面體。
(3) 正多面體:每個面都是有相同邊數的正多邊形,以每個頂點為端點都有相同棱數的凸多面體,叫做正多面體,正多面體只有五種。
(4) 簡單多面體:表面經過連續變形可變為球面的多面體,叫做簡單多面體,如稜柱、稜錐、正多面體等 。